题目内容
6.先化简,再求值:$\frac{{x}^{2}+2x+1}{2x-6}$+(x-$\frac{1-3x}{x-3}$),其中x为方程(x-3)(x-5)=0的根.分析 先算括号里面的,再算加法,求出x的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}+2x+1}{2(x-3)}$+$\frac{{x}^{2}-3x-1+3x}{x-3}$
=$\frac{{x}^{2}+2x+1}{2(x-3)}$+$\frac{{x}^{2}-1}{x-3}$
=$\frac{{x}^{2}+2x+1+2{x}^{2}-2}{2(x-3)}$
=$\frac{2x+3{x}^{2}-1}{2(x-3)}$,
解方程(x-3)(x-5)=0得,x1=3,x2=5,
当x=3时,原式无意义;
当x=5时,原式=$\frac{2×5+3×25-1}{2(5-3)}$=-$\frac{33}{2}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
11.点P(-3,5)关于原点对称的点的坐标是( )
| A. | (3,5) | B. | (-3,-5) | C. | (3,-5) | D. | (-3,5) |
18.一组数据 2,-1,0,-2,x,1 的中位数是0,则x等于( )
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |

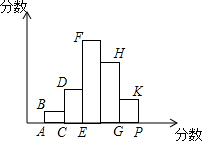 如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.
如图所示,根据某班54个学生的数学成绩绘制的频数分布直方图中,各小长方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后两组为80分以上学生数,则80分以上学生人数是21.