题目内容
17.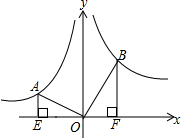 如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.
如图,A,B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上,连接OA、OB,过A、B分别作x轴的垂线,垂足分别为E、F,若OA⊥OB,OB=2OA,则k的值为4.
分析 先证得△AEO∽△OFB,根据相似三角形的性质得出OF=2AE,BF=2OE,设A(a,b),代入y=-$\frac{1}{x}$得出ab=-1,因为OE=-a,AE=b,所以AE•OE=-ab=1,设B(x,y),则OF=x,BF=y,即可求得k=xy=4.
解答 解:∵OA⊥OB,
∴∠AOE+∠BOF=90°,
∵∠AOE+∠OAE=90°,
∴∠BOF=∠OAE,
∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
∴$\frac{AE}{OF}$=$\frac{OE}{BF}$=$\frac{OA}{OB}$=$\frac{1}{2}$,
∴OF=2AE,BF=2OE,
∴OF•BF=2AE•2OE=4AE•OE,
∵A点在反比例函数y=-$\frac{1}{x}$上,
设A(a,b),
∴k=ab=-1,
∵OE=-a,AE=b,
∴AE•OE=-ab=1,
设B(x,y),
∴OF=x,BF=y,
∴OF•BF=4,
∴k=xy=4.
故答案为4.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数y=$\frac{k}{x}$(k≠0)中比例系数k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.

练习册系列答案
相关题目
8.利用平方差公式计算20122-20132的结果是( )
| A. | 1 | B. | -1 | C. | 4025 | D. | -4025 |
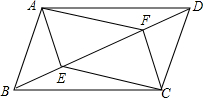 如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:∠EAF=∠FCE.
如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:∠EAF=∠FCE.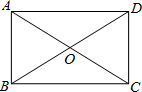 如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.
如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.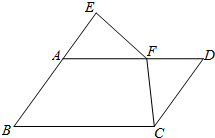 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.