题目内容
7．
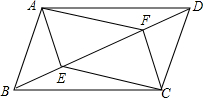如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．求证：∠EAF=∠FCE．
分析 连接AC，交BD于O，根据平行四边形的性质可得AO=CO，BO=DO，再由条件EB=FD可得EO=FO，进而可判定四边形AECF是平行四边形，根据平行四边形的性质可得∠EAF=∠FCE．
解答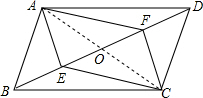 
证明：连接AC，交BD于O，
∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO，
∵BE=DF，
∴EO=FO，
∴四边形AECF是平行四边形，
∴∠EAF=∠FCE．
点评 此题主要考查了平行四边形的判定和性质，关键是掌握平行四边形的对角线互相平分．对角线互相平分的四边形是平行四边形．
练习册系列答案
相关题目
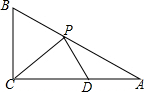如图，在Rt△ABC中，∠ACB=90°，AC=10，BC=5，点P，D分别是线段AB，AC上的两个动点，则PC+PD的最小值为8．
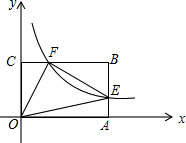如图，在直角坐标系中，双曲线y=$\frac{2}{x}$（x＞0）与矩形OABC的边AB、BC分别交于E、F，AB=nAE（n≥2），m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$．
如图，是某个反比例函数图象的前一部分，A、B为图象上两点，根据图象．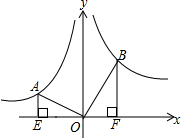
如图，A，B两点分别在反比例函数y=-$\frac{1}{x}$和y=$\frac{k}{x}$的图象上，连接OA、OB，过A、B分别作x轴的垂线，垂足分别为E、F，若OA⊥OB，OB=2OA，则k的值为4．