题目内容

17．抛物线y=x2-6x+5的顶点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用配方法把抛物线的一般式写成顶点式，求顶点坐标；或者用顶点坐标公式求解．

解答 解：∵y=x2-6x+5
=x2-6x+9-9+5
=（x-3）2-4，
∴抛物线y=x2-6x+5的顶点坐标是（3，-4），在第四象限．
故选：D．

点评 此题考查了二次函数的性质，利用配方法求顶点坐标是常用的一种方法．

练习册系列答案
相关题目
7．已知：一次函数y=2x-4．
（1）在直角坐标系内画出一次函数y=2x-4的图象．
（2）当x的值取10时，y为何值？
（3）求函数y=2x-4的图象与坐标轴围成的三角形面积．
8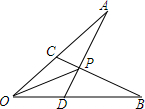．如图，OP平分∠AOB，且OA=OB．则图中全等的三角形为（　　）
A．3对B．4对C．5对D．6对
5．已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点，其对应的数为x．
（1）数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由；
（2）当x为何值时，点P到点A的距离等于点P到点B的距离的2倍？
（3）当x=2时，点A以1个单位长度/秒的速度向左运动，同时点B以2个单位长度/秒向右运动，问多长时间后点P到点A，点B的距离相等？
12．△ABC是等边三角形，点A与点D的坐标分别是A（4，0），D（10，0）．
（1）如图1，当点C与点O重合时，求直线BD的解析式；
（2）如图2，点C从点O沿y轴向下移动，当以点B为圆心，AB为半径的⊙B与y轴相切（切点为C）时，求点B的坐标；
（3）如图3，点C从点O沿y轴向下移动，过点B作BQ⊥x轴，垂足为Q，当点C的坐标为C（0，-2$\sqrt{3}$）时，求$\frac{BQ}{DQ}$的值．
2．将一元二次方程x（x+5）=5x-10化成一般式的形式是（　　）
A．x2+10=0B．x2-10=0C．x2=-10D．x2+50x+10=0
9．方程x2-x=0的常数项是0．
6．在下列选项中，具有相反意义的量是（　　）
A．收入20元与支出30元B．2个苹果和2个梨
C．走了100米又跑了100米D．向东行30米和向北行30米
7．下列运算正确的是（　　）
A．x3•x4=x12B．（x3）4=x12C．x6÷x2=x3D．x3+x4=x7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网