题目内容
9.设n是正整数,且使得$\frac{1}{1+n}$+$\frac{1}{4+n}$+$\frac{1}{9+n}$≥$\frac{1}{7}$,求n的最大值.分析 设s=$\frac{1}{1+n}$+$\frac{1}{4+n}$+$\frac{1}{9+n}$≥$\frac{1}{7}$,根据缩放法得到$\frac{3}{9+n}$<s<$\frac{3}{1+n}$,可得$\frac{3}{1+n}$>$\frac{1}{7}$,解得n的范围,再从大到小找到符合题意的n的最大值.
解答 解:设s=$\frac{1}{1+n}$+$\frac{1}{4+n}$+$\frac{1}{9+n}$≥$\frac{1}{7}$,
∵n是正整数,
∴$\frac{1}{1+n}$>$\frac{1}{4+n}$>$\frac{1}{9+n}$,
∴$\frac{3}{9+n}$<s<$\frac{3}{1+n}$,
则$\frac{3}{1+n}$>$\frac{1}{7}$,
解得n<20,
$\frac{1}{7}$≈0.1429,
当n=19时,s=0.1292<$\frac{1}{7}$;
当n=18时,s=0.1351<$\frac{1}{7}$;
当n=17时,s=0.1416<$\frac{1}{7}$;
当n=16时,s=0.1488>$\frac{1}{7}$;
故n的最大值为16.
点评 此题考查了分式的加减法,解题的关键是得到n的范围,以及分类思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.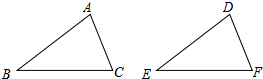 如图,给出下列四组条件:
如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,BC=EF,∠B=∠E;
③∠B=∠E,∠C=∠F,BC=EF;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
 如图,给出下列四组条件:
如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;
②AB=DE,BC=EF,∠B=∠E;
③∠B=∠E,∠C=∠F,BC=EF;
④AB=DE,AC=DF,∠B=∠E.
其中,能使△ABC≌△DEF的条件共有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
14. 如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠AOC,则∠2的度数是( )
如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠AOC,则∠2的度数是( )
 如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠AOC,则∠2的度数是( )
如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠AOC,则∠2的度数是( )| A. | 20° | B. | 25° | C. | 30° | D. | 70° |
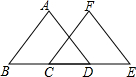 如图,点B、C、D、E在同一直线上,并且BC=DE.若AB=CF,AD=EF.试探索AB与FC的位置关系,并说明理由.
如图,点B、C、D、E在同一直线上,并且BC=DE.若AB=CF,AD=EF.试探索AB与FC的位置关系,并说明理由.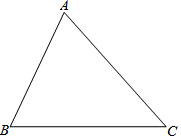 如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.
如图,在某城区地图上,有一块△ABC区域,市政规划要把△ABC区域划分成三个三角形小区域,使任何两个区域都相邻,并且使划分的三个小区域面积彼此相等.请你探究后,把符合题意的示意图画在图中,并说明所画的线是什么线.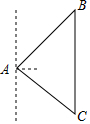 随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.
随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.