题目内容
20.某地召开一场安全级别较高的会议,预估将有4000至7000名人员参加会议,为了确保会议的安全,会议组委会决定对每个入场人员进行安全检查,现了解到安检设各有备有门式安检仪和手持安检仪两种;门式安检仪每台300元,需安检员2名,每分钟可通过10人;手持安检仪每只500元,需要安检员1名,每分钟可通过2人,该会议中心共有6个不同的入口,每个入口都有5条通道可供使用,每条通道只可安放一台门式安检仪或一只手持安检仪,每位安检员的劳务费均为200元(安检总费用包括安检设备费用和安检员的劳务费).现知道会议当日人员从上午9:00开始入场,到上午9:30结束入场,6个入口都采用相同的安检方案,所有人员须提前到达并根据会议通知从相应入口进入.(1)如果每个入口处,只有2个通道安放门式安检仪,而其余3个通道均为手持安检仪,在这个方案下:请问:在规定时间内可通过多少人员?安检所需要的总费用为多少元?
(2)请你设计一个安检方案,确保安检工作的正常进行,同时使得安检所需要的总费用尽可能少.
分析 (1)依题意直接列式计算即可;
(2)设每个门口有x个门式安检仪,则有(5-x)个手持安检仪(0≤n≤5的整数),根据题意列出不等式求出安检方案,用总费用函数关系式确定出安检所需要的总费用最少的方案.
解答 解:(1)在规定时间内通过人数为:6×30×(10×2+2×3)=4680(人),
安检所需要的总费用为:6×[2×300+3×500+(2×2+3×1)×200]=21000(元).
答:在规定时间内可通过4680人,安检所需要的总费用为21000元.
(2)设每个门口有x个门式安检仪,则有(5-x)个手持安检仪,由已知得:
4000≤[30×10x+30×2(5-x)]×6≤7000,
解得:$\frac{55}{36}$≤x≤$\frac{130}{36}$,
∵x为整数,
∴x≥2或3.
由(1)可知,每条通道安放2台门式安检仪时总费用为21000元,
则需要计算每条通道安放3台门式安检仪时总费用:
(300×3+500×2)×6+(200×2×3+200×1×2)×6
=1900×6+1600××6
=21000(元).
综上可知,两种方案的费用一样,
∴设计的方案为:每个入口有2条通道安放2台门式安检仪,3条通道为手持安检仪.
点评 此题是一元一次不等式组的应用,主要考查了列不等式组,解本题的关键是审清题意,列出不等式和函数关系式.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
11.(-$\frac{5}{13}$)2012×$(-2\frac{3}{5})$2012=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 1997 |
8.一艘轮船以16n mile/h的速度从港口A出发向东北方向航行,另一轮船以12n mile/h的速度从港口A出发向东南方向航行,则3h后两船相距( )
| A. | 36n mile | B. | 48n mile | C. | 60n mile | D. | 54n mile |
15.一个长方体的体积为x2-2xy+x,高是x,则这个长方体的底面积是( )
| A. | x-2y | B. | x+2y | C. | x-2y-1 | D. | x-2y+l |
 在学习乘法公式的时候,我们可以通过图形解释加深对公式的理解,下面这个图形可以解释的乘法公式是(a+b)(a-b)=a2-b2.
在学习乘法公式的时候,我们可以通过图形解释加深对公式的理解,下面这个图形可以解释的乘法公式是(a+b)(a-b)=a2-b2.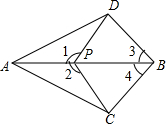 如图,点P在AB上,∠1=∠2,∠3=∠4,求证:DB=CB.
如图,点P在AB上,∠1=∠2,∠3=∠4,求证:DB=CB.