题目内容
10.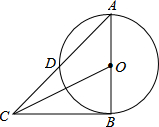 如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.
如图,在⊙O中,AB为直径,AD为弦,过点B的切线与AD的延长线交于点C.已知∠C=40°,则∠DBA的度数是40°.
分析 连接BD,首先由切线的性质可得∠ABC=90°,进而可求∠A得度数,再利用圆周角定理可得∠ADB=90°,所以∠DBA的度数可求出.
解答  解:连接BD,
解:连接BD,
∵过点B的切线与AD的延长线交于点C,AB为直径,
∴AB⊥BC,
∴∠ABC=90°,
∵∠ACB=40°,
∴∠A=50°,
∵AB为直径,
∴∠ADB=90°,
∴∠DBA=90°-50°=40°,
故答案为:40°.
点评 本题考查了切线的性质、三角形的内角和定理、圆周角定理等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
19.小馨和小霏是七(1)班的学生,两人既是好朋友,又是学习上的竞争对手.她们约定在本次的期末考试中比一比谁的总分高.(考试科目见下表,每门课的满分为100分,单科分数均为整数)下表是她们期末考试的部分成绩.
根据表格显示的数据,小霏同学数学成绩至少91 分,她的总分才有可能比小馨总分高.
| 姓名 | 语文 | 数学 | 英语 | 政治 | 历史 |
| 小馨 | 86 | 98 | 100 | 96 | 97 |
| 小霏 | 88 | 99 |
 如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么?
如图,如果AB∥CD,∠B=30°,∠D=30°,那么BC与DE平行吗?为什么? 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: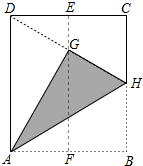 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.
如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为2$\sqrt{3}$cm.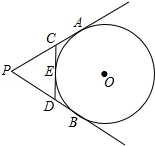 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则sin∠APB的值是$\frac{12}{13}$.