题目内容
2.一次函数y=kx+k-3,当k=3时,图象过原点;当k>0时,y随x的增大而增大.分析 分别根据正比例函数与一次函数的性质进行解答即可.
解答 解:∵一次函数y=kx+k-3经过原点,
∴k-3=0,解得k=3;
∵y随x的增大而增大,
∴k>0.
故答案为:3,>0.
点评 本题考查的是一次函数图象上点的坐标特点,熟知正比例函数与一次函数的性质是解答此题的关键.

练习册系列答案
相关题目
15. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )| A. | 两根都大于0 | B. | 两根都等于0 | ||
| C. | 两根都小于0 | D. | 一根大于0,一根小于0 |
17.下面用数学语言叙述$\frac{1}{a}$-b,其中表达不正确的是( )
| A. | 比a的倒数小b的数 | B. | 1除以a的商与b的绝对值的差 | ||
| C. | 1除以a的商与b的相反数的和 | D. | b与a的倒数的差的相反数 |
10.下列计算中,正确的是( )
| A. | (a+b)2=a2+b2 | B. | (x-3y)2=x2-3xy+9y2 | ||
| C. | (6a3-4a2+2a)÷2a=3a2-2a | D. | ab2÷a=b2 |
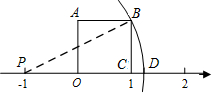 如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1.
如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1.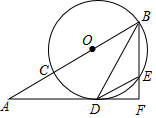 过⊙O的直径BC的延长线上一点A作圆的切线,D为切点,过B作切线的垂线交圆于点E,F为垂足,AC=DE,求AC和AB的比值.
过⊙O的直径BC的延长线上一点A作圆的切线,D为切点,过B作切线的垂线交圆于点E,F为垂足,AC=DE,求AC和AB的比值. 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,BC=12,则DE的长是( )