题目内容
3.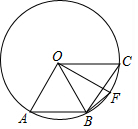 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( )| A. | 12.5° | B. | 15° | C. | 20° | D. | 22.5° |
分析 先根据平行四边形的性质得出AB=BC,故可得出△OAB是等边三角形,所以∠AOB=60°,再由OF⊥OA可知∠AOF=90°,OF⊥BC,故可得出∠BOF的度数,进而得出∠COF的度数,由圆周角定理即可得出结论.
解答 解:∵四边形ABCO是平行四边形,
∴AB=BC,OA∥BC.
∵OA=OC,
∴△OAB是等边三角形,
∴∠AOB=60°.
∵OF⊥OA,
∴∠AOF=90°,OF⊥BC,
∴∠BOF=∠COF=90°-60°=30°,
∴∠CBF=$\frac{1}{2}$∠COF=15°.
故选B.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
16.若|a|=8,|b|=5,且a>0,b<0,a-b的值是( )
| A. | 3 | B. | -3 | C. | 13 | D. | -13 |
14.一元二次方程5x2-11x+4=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
18.下列代数式符合书写要求的是( )
| A. | a+5 | B. | 5$\frac{3}{4}$a | C. | ab5 | D. | a÷b |
8.如图图案中,可以看做是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的根的情况( )| A. | 两根都大于0 | B. | 两根都等于0 | ||
| C. | 两根都小于0 | D. | 一根大于0,一根小于0 |
12. 如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
 如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )
如图,要使六边形木架(用六根木条钉成)不变形,至少要再钉上木条的根数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
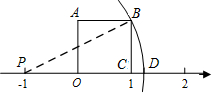 如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1.
如图,正方形OABC的边OC落在数轴上,点C表示的数为1,点P表示的数为-1,以 P点为圆心,PB长为半径作圆弧与数轴交于点D,则点D表示的数为$\sqrt{5}$-1.