题目内容
17.下列一元二次方程中,有两个不相等实数根的方程是( )| A. | x2+1=0 | B. | x2-3x+1=0 | C. | x2-2x+1=0 | D. | x2-x+1=0 |
分析 根据一元二次方程根的判别式,分别计算△的值,逐一进行判断即可.
解答 解:A、△=-4<0,方程没有实数根;
B、△=9-4=5>0,方程有两个不相等的实数根;
C、△=4-4=0,方程有两个相等实数根;
D、△=1-4=-3<0,方程没有实数根.
故选:B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{0.5mn}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{27}$ | D. | $-\sqrt{125}$ |
9.一个正多边形的每个外角都是36°,则这个正多边形的内角和为( )
| A. | 1800° | B. | 1620° | C. | 1440° | D. | 1260° |
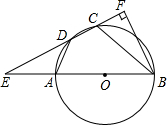 已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.
已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.
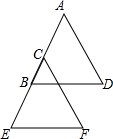 如图已知,A、B、C、E四点在一直线上,AC=BE,AD=CF,BD=EF,试说明BD∥EF.
如图已知,A、B、C、E四点在一直线上,AC=BE,AD=CF,BD=EF,试说明BD∥EF.