题目内容
6.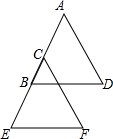 如图已知,A、B、C、E四点在一直线上,AC=BE,AD=CF,BD=EF,试说明BD∥EF.
如图已知,A、B、C、E四点在一直线上,AC=BE,AD=CF,BD=EF,试说明BD∥EF.
分析 利用已知条件证明△ABD≌△CEF,得到∠B=∠E,再根据平行线的判定即可解答.
解答 解:∵AC=BE,
∴AC+BC=BE+BC,
即AB=CE,
在△ABD和△CEF中,
$\left\{\begin{array}{l}{AB=CE}\\{AD=CF}\\{BD=EF}\end{array}\right.$
∴△ABD≌△CEF,
∴∠B=∠E,
∴BD∥EF.
点评 本题主要考查了全等三角形的判定与性质和平行线的判定,解决本题的关键是证明△ABD≌△CEF.

练习册系列答案
相关题目
17.下列一元二次方程中,有两个不相等实数根的方程是( )
| A. | x2+1=0 | B. | x2-3x+1=0 | C. | x2-2x+1=0 | D. | x2-x+1=0 |
1.一次体检中,某班学生的视力情况如表所示,从表中可以看出全班视力情况的众数是( )
| 视力情况 | 4.6及以下 | 4.7 | 4.8 | 4.9 | 5.0 | 5.0以上 |
| 人数所占的百分比 | 5% | 8% | 15% | 20% | 40% | 12% |
| A. | 4.85 | B. | 5.0 | C. | 40% | D. | 5.3 |
11.-$\frac{3}{4}$的绝对值是( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
18.已知a+b=5,ab=4,则代数式(3ab+5a+8b)+(3a-4ab)的值为( )
| A. | 36 | B. | 40 | C. | 44 | D. | 46 |
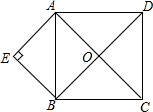 如图,点O为正方形ABCD的对角线的交点,E为正方形外一点,且AE⊥BE.
如图,点O为正方形ABCD的对角线的交点,E为正方形外一点,且AE⊥BE. 如图,若∠1=40°,∠2=40°,∠3=120°,则∠4=60°.
如图,若∠1=40°,∠2=40°,∠3=120°,则∠4=60°.