题目内容
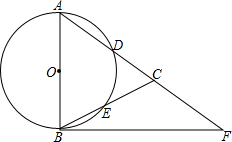 如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.(1)求证:∠CBF=
| 1 |
| 2 |
(2)若AB=5,sin∠CBF=
| ||
| 5 |
考点:切线的性质
专题:
分析:(1)连接AE,由圆周角定理和等腰三角形的性质,结合切线的性质可证得∠CBF=∠BAE,可证得结论;
(2)由(1)结论结合正弦值,在Rt△ABE中可求得BE,可求出BC,过C作CM⊥BF,在Rt△BCM中可求得BM,CM,再利用平行线分线段成比例可求得BF.
(2)由(1)结论结合正弦值,在Rt△ABE中可求得BE,可求出BC,过C作CM⊥BF,在Rt△BCM中可求得BM,CM,再利用平行线分线段成比例可求得BF.
解答:(1)证明:如图1,连结AE.
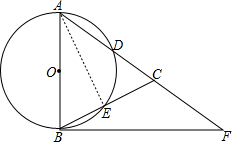
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAE=
∠BAC.
∵BF是⊙O的切线,
∴∠CBF=∠BAE,
∴∠CBF=
∠CAB.
(2)解:由(1)可知∠CBF=∠BAE,
∴sin∠BAE=sin∠CBF=
,
在Rt△ABE中,sin∠BAE=
,
∴
=
,
∴BE=
,
∴BC=2
,
如图2,过C作CM⊥BF于点M,
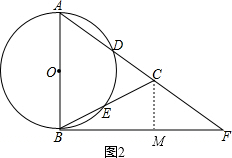
则sin∠CBF=
=
,
即
=
,解得CM=2,由勾股定理可求得BM=4,
又∵AB∥CM,
∴
=
,
即
=
,解得BF=
.

∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠BAE=
| 1 |
| 2 |
∵BF是⊙O的切线,
∴∠CBF=∠BAE,
∴∠CBF=
| 1 |
| 2 |
(2)解:由(1)可知∠CBF=∠BAE,
∴sin∠BAE=sin∠CBF=
| ||
| 5 |
在Rt△ABE中,sin∠BAE=
| BE |
| AB |
∴
| BE |
| 5 |
| ||
| 5 |
∴BE=
| 5 |
∴BC=2
| 5 |
如图2,过C作CM⊥BF于点M,

则sin∠CBF=
| CM |
| BC |
| ||
| 5 |
即
| CM | ||
2
|
| ||
| 5 |
又∵AB∥CM,
∴
| CM |
| AB |
| BF-BM |
| BF |
即
| 2 |
| 5 |
| BF-4 |
| BF |
| 20 |
| 3 |
点评:本题主要考查切线的性质及等腰三角形的性质、三角函数的定义等知识点,掌握弦切角定理及三角函数的定义是解题的关键,注意平行线分线段定理的应用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知
=
,则x的值是( )
| 3 |
| x |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 四边形ABCD中,AB=BC,BE丄AD垂足为E,∠BCD-∠ABE=90°.过点C作CF∥AD交对角线BD于F,求证:CF=CD.
四边形ABCD中,AB=BC,BE丄AD垂足为E,∠BCD-∠ABE=90°.过点C作CF∥AD交对角线BD于F,求证:CF=CD. 如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.
如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.