题目内容
3.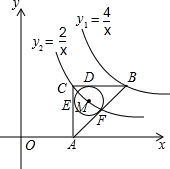 如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).
如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
分析 (1)先求得点C的坐标,然后根据平行于x轴上点纵坐标相等,可知点B的纵坐标,然后可求得点B的横坐标;
(2)连接MD、ME、MF.由点B和点C的坐标可求得AC、BC的长,依据勾股定理可求得AB的长,然后在△ABC中利用面积法可求得圆M的半径,从而可求得点M的坐标.
解答 解:(1)∵CA⊥x轴,∠ACB=90°,
∴CB∥x轴.
∵将C($\sqrt{2}$,m)代入函数y2=$\frac{2}{x}$得:n=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴点C($\sqrt{2}$,$\sqrt{2}$).
∴点B的纵坐标为$\sqrt{2}$.
∵将y1=$\sqrt{2}$代入得:$\frac{4}{x}$=$\sqrt{2}$,解得;x=2$\sqrt{2}$,
∴点B的坐标为(2$\sqrt{2}$,$\sqrt{2}$).
(2)如图所示:连接ME、MD、MF.
∵⊙M与BC,CA,AB分别相切于D,E,F,
∴ME⊥AC,MD⊥BC,MF⊥AB.
∴∠ECD=∠CDM=∠CEM=90°.
∴四边形CDME为矩形.
∵MD=ME,
∴四边形CDME为正方形.
∵在Rt△ACB中,AC=$\sqrt{2}$,BC=$\sqrt{2}$,
∴AB=2.
∵S△ACB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$(AC+BC+AB)•r,
∴⊙M的半径=$\frac{AC•BC}{AC+BC+AB}$=$\frac{\sqrt{2}×\sqrt{2}}{2\sqrt{2}+2}$=$\sqrt{2}$-1.
∴点M的坐标为(2$\sqrt{2}$-1,1).
点评 本题主要考查的是反比例函数的综合应用,解答本题主要应用了反比例函数图象上的点与函数解析式的关系、平行与坐标轴上的点的坐标特点、三角形的内切圆、正方形的性质和判定,求得⊙M的半径是解题的关键.

| A. | $\frac{a+b}{b}=\frac{3}{2}$ | B. | $\frac{a+2c}{b+2d}=2$ | C. | $\frac{a-c}{b-d}=\frac{1}{2}$ | D. | b=2a |
| A. | a-(2b-3c)=-(a+2b-3c) | B. | x3-b和-x3-b互为相反数 | ||
| C. | 当x<0时,|3x-x|=-2x | D. | 1×(-1)+2÷(-1)-(-1)=0 |
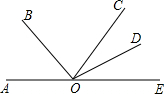 如图,点A、O、E在同一直线上,∠AOB=40°,OD平分∠COE,∠BOC=3∠COD+10°,求∠BOC的度数.
如图,点A、O、E在同一直线上,∠AOB=40°,OD平分∠COE,∠BOC=3∠COD+10°,求∠BOC的度数.