题目内容
10.解方程组①$\left\{\begin{array}{l}{2x+y=3}\\{3x-5y=11}\end{array}\right.$; ②$\left\{\begin{array}{l}{x-y=6}\\{5x+2y=2}\end{array}\right.$.
分析 两方程组利用加减消元法求出解即可.
解答 解:①$\left\{\begin{array}{l}{2x+y=3①}\\{3x-5y=11②}\end{array}\right.$,
①×5+②得:13x=26,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
②$\left\{\begin{array}{l}{x-y=6①}\\{5x+2y=2②}\end{array}\right.$,
①×2+②得:7x=14,即x=2,
把x=2代入①得:y=-4,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
20.小亮在匀速行驶的汽车里,注意到公路里程碑上的数如下:
则12:00时看到的两位数是27.
| 时刻 | 12:00 | 13:00 | 16:00 |
| 碑上的数 | 是一个两位数 | 十位与个位数字与12:00时 所看到的正好颠倒了 | 比12:00时看到的两位数 中间多了个0 |
18.若∠1与∠2是同旁内角,∠1=40°,则∠2的度数是( )
| A. | 40° | B. | 140° | C. | 40°或140° | D. | 不能确定 |
 如图,将两张长为6cm,宽为3cm的矩形纸条交叉,使重叠部分是一个菱形,那么菱形周长的最大值是15.
如图,将两张长为6cm,宽为3cm的矩形纸条交叉,使重叠部分是一个菱形,那么菱形周长的最大值是15. 如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )
如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )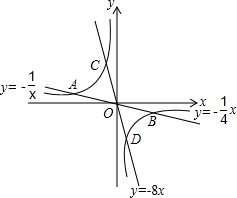 如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.