题目内容
7.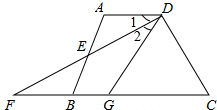 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.(1)求证:△ADE≌△BFE;
(2)联结EG,试说明EG与DF垂直的理由.
分析 (1)由AD与BC平行,利用两直线平行内错角相等,得到一对角相等,再由一对对顶角相等及E为AB中点得到一对边相等,利用AAS即可得出△ADE≌△BFE;
(2)由∠GDF=∠ADE,以及(1)得出的∠ADE=∠BFE,等量代换得到∠GDF=∠BFE,利用等角对等边得到GF=GD,即三角形GDF为等腰三角形,再由(1)得到DE=FE,即GE为底边上的中线,利用三线合一即可得到GE与DF垂直.
解答 解:(1)∵AD∥BC,
∴∠1=∠F(两直线平行,内错角相等)
∵E为AB的中点,
∴AE=BE(中点的意义),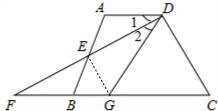
在△ADE和△BFE中,$\left\{\begin{array}{l}∠1=∠F(已证)\\∠AED=∠BEF(对顶角相等)\\ AE=BE(已知)\end{array}\right.$
∴△ADE≌△BFE(AAS).
(2)∵∠1=∠F,∠1=∠2,
∴∠F=∠2(等量代换),
∴DG=FG(等角对等边).
∵△ADE≌△BFE (已证),
∴DE=FE(全等三角形的对应边相等),
∴EG⊥DF(等腰三角形三线合一).
点评 此题考查了全等三角形的判定与性质,平行线的性质,以及等腰三角形的判定与性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
17.下列四个多项式,哪一个是2x2+4x+2的因式?( )
| A. | 2x-1 | B. | 2x-3 | C. | x+1 | D. | x-3 |
18.若∠1与∠2是同旁内角,∠1=40°,则∠2的度数是( )
| A. | 40° | B. | 140° | C. | 40°或140° | D. | 不能确定 |
12.某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
(1)分别求出甲、乙、丙三人的面试成绩的平均分$\overline{甲}$、$\overline{乙}$和$\overline{丙}$;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
| 候选人 | 评委1 | 评委2 | 评委3 |
| 甲 | 94 | 89 | 90 |
| 乙 | 92 | 90 | 94 |
| 丙 | 91 | 88 | 94 |
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.
17.用配方法解方程x2-8x+9=0时,原方程可变形为( )
| A. | (x-4)2=9 | B. | (x-4)2=7 | C. | (x-4)2=-9 | D. | (x-4)2=-7 |
 如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )
如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )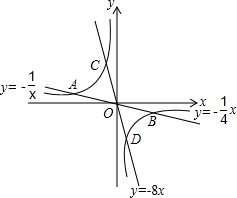 如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$. 如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=180°.
如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3=180°.