题目内容
20.方程:(2x+1)(x-1)=8(9-x)-1的根为-8或$\frac{9}{2}$.分析 首先去括号,进而合并同类项,再利用十字相乘法分解因式得出即可.
解答 解:(2x+1)(x-1)=8(9-x)-1
整理得:2x2-x-1=72-8x-1
2x2+7x-72=0,
则(x+8)(2x-9)=0,
解得:x1=-8,x2=$\frac{9}{2}$.
故答案为:-8或$\frac{9}{2}$.
点评 此题主要考查了因式分解法解方程,正确利用十字相乘法分解因式是解题关键.

练习册系列答案
相关题目
15.某商店需要购进甲、乙两种商品共120件,其进价和售价如下表:(注:获利=售价-进价)
(1)若商店计划销售完这批商品后能获利1000元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4000元,且销售完这批商品后获利多于1135元,请问有哪几种购货方案?并指出获利最大的购货方案.
| 甲 | 乙 | |
| 进价(元/件) | 15 | 35 |
| 售价(元/件) | 20 | 45 |
(2)若商店计划投入资金少于4000元,且销售完这批商品后获利多于1135元,请问有哪几种购货方案?并指出获利最大的购货方案.
10.在?ABCD中,AC与BD相交于点O,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AO}$等于( )
| A. | $\overrightarrow a+\overrightarrow b$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC. 已知:△ABC中,∠B=2∠C,AD⊥BC,E为BC的中点,求证:AB=2DE.
已知:△ABC中,∠B=2∠C,AD⊥BC,E为BC的中点,求证:AB=2DE.
 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是5.
如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是5.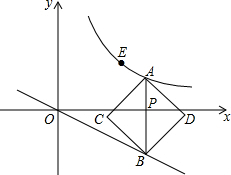 如图,在直角坐标系中,已知点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上.过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=-$\frac{1}{2}$x交于A、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为2或$\frac{2}{3}$.
如图,在直角坐标系中,已知点E(3,2)在双曲线y=$\frac{k}{x}$(x>0)上.过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=-$\frac{1}{2}$x交于A、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为2或$\frac{2}{3}$.