题目内容
已知△ABC中,∠A=150°,AB=2
,AC=2,求△ABC的面积及BC的长.
| 3 |
考点:解直角三角形
专题:
分析:过C作AB边上高CD,易求得AD,CD的长,即可求得△ABC的面积,由AB,AD的长可求得BD的长,再根据勾股定理即可求得BC的长.
解答:解:过C作AB边上高CD,

∵∠BAC=150°,∴∠CAD=30°,
∵AC=2,∴CD=
AC=1,AD=AC•cos30°=
,
∴BD=AD+AB=3
,
∴△ABC的面积=
AB•CD=2
,
∵BC2=CD2+BD2=28,
∴BC=2
.

∵∠BAC=150°,∴∠CAD=30°,
∵AC=2,∴CD=
| 1 |
| 2 |
| 3 |
∴BD=AD+AB=3
| 3 |
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
∵BC2=CD2+BD2=28,
∴BC=2
| 7 |
点评:本题考查了勾股定理在直角三角形中运用,考查了直角三角形中三角函数的运用,考查了特殊角的三角函数值,本题中求得CD,AD的长是解题的关键.

练习册系列答案
相关题目
抛物线y=2(x+3)2的顶点坐标是( )
| A、(3,0) |
| B、(0,3) |
| C、(-3,0) |
| D、(0,-3) |
 如图,在平行四边形ABCD中,E是AB延长线上一点,连接DE,交AC于点G,交BC于点F,那么图中相似三角形(不含全等三角形)共有( )
如图,在平行四边形ABCD中,E是AB延长线上一点,连接DE,交AC于点G,交BC于点F,那么图中相似三角形(不含全等三角形)共有( )| A、6对 | B、5对 | C、4对 | D、3对 |
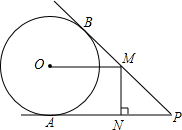 如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N. 如图,O是直线AB上一点,OD是∠AOC的平分线,OE⊥OD.OE是∠BOC的平分线吗?为什么?
如图,O是直线AB上一点,OD是∠AOC的平分线,OE⊥OD.OE是∠BOC的平分线吗?为什么? 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=