题目内容
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=| 1 |
| 4 |
考点:相似三角形的判定
专题:
分析:先根据题意判断出△ABE∽△ECF,故可得出AB:EC=AE:EF,∠AEB=∠EFC,再由BE=CE,∠FEC+∠EFC=90°可知AB:AE=BE:EF,∠AEB+∠FEC=90°,故可得出结论.
解答:证明:∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=
CD,
∴∠B=∠C=90°,AB:EC=BE:CF=2:1.
∴△ABE∽△ECF.
∴AB:EC=AE:EF,∠AEB=∠EFC.
∵BE=CE,∠FEC+∠EFC=90°,
∴AB:AE=BE:EF,∠AEB+∠FEC=90°.
∴∠AEF=∠B=90°.
∴△ABE∽△AEF.
| 1 |
| 4 |
∴∠B=∠C=90°,AB:EC=BE:CF=2:1.
∴△ABE∽△ECF.
∴AB:EC=AE:EF,∠AEB=∠EFC.
∵BE=CE,∠FEC+∠EFC=90°,
∴AB:AE=BE:EF,∠AEB+∠FEC=90°.
∴∠AEF=∠B=90°.
∴△ABE∽△AEF.
点评:此题考查了相似三角形的判定,熟知有两个对应角相等的三角形相似;有两个对应边的比相等,且其夹角相等,则两个三角形相似;三组对应边的比相等,则两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
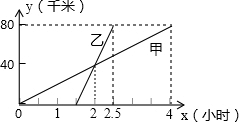 甲乙两人分别骑自行车和摩托车沿相同路线由A地到B地,图中表示他们在行驶过程中距A地的路程y(千米)和时间t(时)函数关系的图象.
甲乙两人分别骑自行车和摩托车沿相同路线由A地到B地,图中表示他们在行驶过程中距A地的路程y(千米)和时间t(时)函数关系的图象. 在等腰Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE且AD⊥AC,连接EC,取EC的中点M,连结DM和BM,结论:△BMD为等腰直角三角形成立吗?
在等腰Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE且AD⊥AC,连接EC,取EC的中点M,连结DM和BM,结论:△BMD为等腰直角三角形成立吗?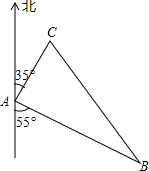 如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?
如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?