题目内容
在△ABC中,已知∠A、∠B、∠C的度数比为1:2:3,边AB上的中线长为1,则此三角形最短边长为 .
考点:含30度角的直角三角形,直角三角形斜边上的中线
专题:
分析:根据三角形内角和定理求出三角形ABC是直角三角形,求出∠A=30°,求出AB,再求出BC即可.
解答:解:
∵∠A、∠B、∠C的度数比为1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ACB是直角三角形,
∵中线CD=1,
∴AB=2CD=2,
∴BC=
AB=1,
故答案为:1

∵∠A、∠B、∠C的度数比为1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ACB是直角三角形,
∵中线CD=1,
∴AB=2CD=2,
∴BC=
| 1 |
| 2 |
故答案为:1
点评:本题考查了三角形内角和定理,直角三角形斜边上中线性质,含30度角的直角三角形性质的应用,解此题的关键是求出△ABC是直角三角形、求出∠A的度数和AB的值.

练习册系列答案
相关题目
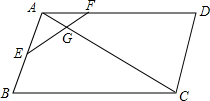 已知平行四边形ABCD,E为AB中点,EF交AC于G点,
已知平行四边形ABCD,E为AB中点,EF交AC于G点,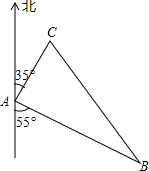 如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?
如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?