题目内容
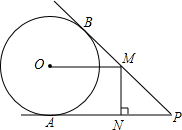 如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
如图,PA、PB分别与⊙O相切于点A、B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.(1)求证:OM=AN;
(2)若⊙O的半径R=3,PA=8,求OM的长.
考点:切线的性质
专题:证明题
分析:(1)连结OA,如图,先根据切线的性质得到∠OAP=90°,再证明四边形ANMO为矩形,然后根据矩形的性质得到结论;
(2)解:连结OB,如图,先根据切线的性质得到∠OBM=90°,再利用四边形ANMO为矩形得到MN=OA=3,OM=AN,接着可证明△PMN≌△MOB,则PM=OM,所以OM=AN=PM,
根据切线长定理得PA=PB=8,然后设OM=x,则PN=8-x,PM=x,在Rt△PMN中利用勾股定理得到32+(8-x)2=x2,再解方程求出x即可.
(2)解:连结OB,如图,先根据切线的性质得到∠OBM=90°,再利用四边形ANMO为矩形得到MN=OA=3,OM=AN,接着可证明△PMN≌△MOB,则PM=OM,所以OM=AN=PM,
根据切线长定理得PA=PB=8,然后设OM=x,则PN=8-x,PM=x,在Rt△PMN中利用勾股定理得到32+(8-x)2=x2,再解方程求出x即可.
解答:(1)证明:连结OA,如图,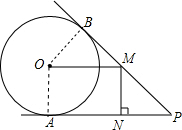
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵OM∥AP,
∴∠AOM=90°,
而MN⊥PA,
∴∠MNA=90°,
∴四边形ANMO为矩形,
∴OM=AN;
(2)解:连结OB,如图,
∵PB为⊙O的切线,
∴OB⊥PA,OB=3,
∴∠OBM=90°,
∵四边形ANMO为矩形,
∴MN=OA=3,OM=AN,
∴OB=MN,
∵OM∥PA,
∴∠MPN=∠BMO,
在△PMN和△MOB中,
,
∴△PMN≌△MOB(AAS),
∴PM=OM,
∴OM=AN=PM,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB=8,
设OM=x,则PN=8-x,PM=x,
在Rt△PMN中,∵MN2+PN2=PM2,
∴32+(8-x)2=x2,解得x=
,
即OM的长为
.

∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵OM∥AP,
∴∠AOM=90°,
而MN⊥PA,
∴∠MNA=90°,
∴四边形ANMO为矩形,
∴OM=AN;
(2)解:连结OB,如图,
∵PB为⊙O的切线,
∴OB⊥PA,OB=3,
∴∠OBM=90°,
∵四边形ANMO为矩形,
∴MN=OA=3,OM=AN,
∴OB=MN,
∵OM∥PA,
∴∠MPN=∠BMO,
在△PMN和△MOB中,
|
∴△PMN≌△MOB(AAS),
∴PM=OM,
∴OM=AN=PM,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB=8,
设OM=x,则PN=8-x,PM=x,
在Rt△PMN中,∵MN2+PN2=PM2,
∴32+(8-x)2=x2,解得x=
| 73 |
| 16 |
即OM的长为
| 73 |
| 16 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和全等三角形的判定与性质.

练习册系列答案
相关题目
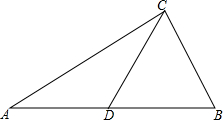 已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.
已知:如图,△ABC中,D是AB中点,若AC=12,BC=5,CD=6.5,求证:△ABC是直角三角形.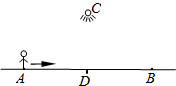 如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.
如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.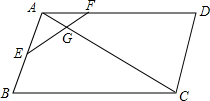 已知平行四边形ABCD,E为AB中点,EF交AC于G点,
已知平行四边形ABCD,E为AB中点,EF交AC于G点,