题目内容
 如图,O是直线AB上一点,OD是∠AOC的平分线,OE⊥OD.OE是∠BOC的平分线吗?为什么?
如图,O是直线AB上一点,OD是∠AOC的平分线,OE⊥OD.OE是∠BOC的平分线吗?为什么?考点:垂线,角平分线的定义
专题:
分析:OE是∠BOC的平分线.由于∠AOB是平角,OD是∠AOC的平分线,∠DOE=90°,易求∠COE+∠AOC=∠BOE+∠AOD,即∠COE=∠BOE.
解答:解:OE是∠BOC的平分线,理由如下:
∵OD是∠AOC的平分线,OE⊥OD,
∴∠AOD=∠COD,∠DOE=90°,
∴∠AOD+∠BOE=90°,
∴∠COE+∠AOC=∠BOE+∠AOD,即∠COE=∠BOE.
∴OE是∠BOC的平分线.
∵OD是∠AOC的平分线,OE⊥OD,
∴∠AOD=∠COD,∠DOE=90°,
∴∠AOD+∠BOE=90°,
∴∠COE+∠AOC=∠BOE+∠AOD,即∠COE=∠BOE.
∴OE是∠BOC的平分线.
点评:本题考查了角的计算.解题的关键是理解角平分线的定义.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
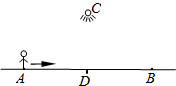 如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.
如图,夜晚,小亮从点A出发,经过路灯C的正下方点D,沿直线走到点B停止,他的影长y随他与点A之间的距离x的变化而变化.已知小亮的身高为1.6m,路灯C与地面的距离CD为4.8m,AD=BD=60m,求出y与x之间的函数表达式,并写出自变量的取值范围.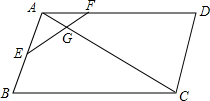 已知平行四边形ABCD,E为AB中点,EF交AC于G点,
已知平行四边形ABCD,E为AB中点,EF交AC于G点, 如图,△ABC内有并排的n个相等的小正方形,它们组成的矩形内接于△ABC.已知BC=10,BC边上的高为6,则小正方形的边长等于
如图,△ABC内有并排的n个相等的小正方形,它们组成的矩形内接于△ABC.已知BC=10,BC边上的高为6,则小正方形的边长等于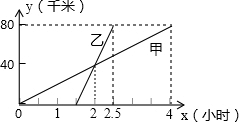 甲乙两人分别骑自行车和摩托车沿相同路线由A地到B地,图中表示他们在行驶过程中距A地的路程y(千米)和时间t(时)函数关系的图象.
甲乙两人分别骑自行车和摩托车沿相同路线由A地到B地,图中表示他们在行驶过程中距A地的路程y(千米)和时间t(时)函数关系的图象. 如图,点A、O、B在同一条直线上,射线OD平分∠BOC,若∠BOC=40°,则∠AOD=
如图,点A、O、B在同一条直线上,射线OD平分∠BOC,若∠BOC=40°,则∠AOD=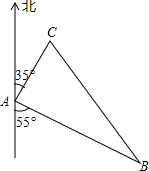 如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?
如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛;若C、B两岛相距48海里,问乙船的航速是每小时多少海里?