题目内容
7. 如图,将半径为6的⊙O沿AB折叠,$\widehat{AB}$与AB垂直的半径OC交于点D且CD=2OD,则折痕AB的长为8$\sqrt{2}$.
如图,将半径为6的⊙O沿AB折叠,$\widehat{AB}$与AB垂直的半径OC交于点D且CD=2OD,则折痕AB的长为8$\sqrt{2}$.
分析 延长CO交AB于E点,连接OB,构造直角三角形,然后再根据勾股定理求出AB的长
解答 解:延长CO交AB于E点,连接OB,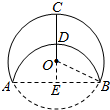
∵CE⊥AB,
∴E为AB的中点,
∵OC=6,CD=2OD,
∴CD=4,OD=2,OB=6,
∴DE=$\frac{1}{2}$(2OC-CD)=$\frac{1}{2}$(6×2-4)=$\frac{1}{2}$×8=4,
∴OE=DE-OD=4-2=2,
在Rt△OEB中,
∵OE2+BE2=OB2,
∴BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
∴AB=2BE=8$\sqrt{2}$.
故答案为:8$\sqrt{2}$.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.二次函数y=(x-$\frac{1}{m}$)•(mx-6m),其中m>0,下列结论正确的是( )
| A. | 该函数图象与坐标轴必有三个交点 | |
| B. | 当m>3时,都有y随x的增大而增大 | |
| C. | 若当x<n,都有y随着x的增大而减小,则n≤3+$\frac{1}{2m}$ | |
| D. | 该函数图象与直线y=-x+6的交点随着m的取值变化而变化 |
12.按如图所示的程序计算,若开始输入的x值为5,则最后输出的结果是( )


| A. | 15 | B. | 120 | C. | 160 | D. | 以上答案均不对 |
17.如果$\sqrt{y}$=1.5,那么y的值是( )
| A. | 2.25 | B. | 22.5 | C. | 2.55 | D. | 25.5 |
 一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E.
一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E. 如图,△ADE∽△ABC,$\frac{AD}{BD}$=$\frac{1}{2}$,△ABC的面积为18,求四边形BCED的面积.
如图,△ADE∽△ABC,$\frac{AD}{BD}$=$\frac{1}{2}$,△ABC的面积为18,求四边形BCED的面积. 如图,已知ED⊥DB于点D,AB⊥DB于点B,ED=CB,DC=AB,则EC与AC的关系是相等.
如图,已知ED⊥DB于点D,AB⊥DB于点B,ED=CB,DC=AB,则EC与AC的关系是相等.