题目内容
若x2+2（m﹣1）x+36是完全平方式，则m=__．
7或﹣5
【解析】∵x2+2（m﹣1）x+36是完全平方式，
∴2（m﹣1）x=±2×6x,
∴m﹣1=±6,
∴m=7或m=-5.
练习册系列答案
相关题目
已知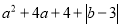
=0，则a+b=__________.
1
【解析】∵a2+4a+4+|b-3|=0，∴(a+2)2+|b-3|=0，∴a+2=0，b-3=0，∴a=-2，b=3，∴a+b=1，
故答案为：1. 在直角坐标系中，将点P(－3,2)向沿y轴方向向上平移4个单位长度后，得到的点坐标为( )
A. (－3,6) B. (1,2) C. (－7,2) D. (－3，－2)
A
【解析】因为点沿y轴向上移动,横坐标不变,纵坐标加上平移单位,将点P(－3,2)向沿y轴方向向上平移4个单位长度后,得到的点坐标为(－3,6),故选A. 二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）
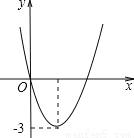
A. -3 B. 3 C. -6 D. 9
B
【解析】先根据抛物线的开口向上可知a＞0，由顶点纵坐标为-3得出b与a关系，再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式，求出m的取值范围即可．
【解析】
∵抛物线的开口向上，顶点纵坐标为-3，
∴a＞0， =-3，即b2=12a，
∵一元二次方程ax2+bx+m=0有实数根，
∴△=b2-4am≥0，即12a-4am≥0，即12-4m≥0，解得m≤3... 如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（ ）
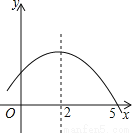
A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5
D
【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0），
∴函数图象与x轴的另一交点坐标为（-1，0），
∴ax2+bx+c＜0的解集是x＜-1或x＞5．
故选C. 5x2﹣25x2y的公因式为__．
5x2
【解析】∵5x2﹣25x2y=5x2(1-y),
∴5x2﹣25x2y的公因式为5x2. 下列各式从左到右的变形中，是因式分解的是（ ）.
A. x（a-b）=ax-bx B. x2-1+y2=（x-1）（x+1）+y2
C. y2-1=（y+1）（y-1） D. ax+bx+c=x（a+b）+c
C
【解析】A. 是整式的乘法，故A错误；
B. 没把一个多项式转化成几个整式积，故B错误；
C. 把一个多项式转化成几个整式积，故C正确；
D. 没把一个多项式转化成几个整式积，故D错误；
故选：C. 下列图形中，不是轴对称图形的是（ ）
A. 有两个内角相等的三角形 B. 有一个内角为45°的直角三角形
C. 有两个内角分别为50°和80°的三角形 D. 有两个内角分别为55°和65°的三角形
D
【解析】A.有两个内角相等的三角形是等腰三角形，等腰三角形是轴对称图形；
B.有一个内角为45度的直角三角形是等腰直角三角形，也是等腰三角形，是轴对称图形；C.有两个内角分别为50度和80度的三角形，第三个角是50度，故是等腰三角形，是轴对称图形；
D.有两个内角分别为55度和65度的三角形,不是等腰三角形，不是轴对称图形.
故选：D. 每年六七月份我市荔枝大量上市，今年某水果商以5元/千克的价格购进一批荔枝进行销售，运输过程中质量损耗5%，运输费用是0.7元/千克，假设不计其他费用．
（1）水果商要把荔枝售价至少定为多少才不会亏本？
（2）在销售过程中，水果商发现每天荔枝的销售量m（千克）与销售单价x（元/千克）之间满足关系：m= -10x+120，那么当销售单价定为多少时，每天获得的利润w最大？
（1）水果商要把荔枝售价至少定为6元/千克才不会亏本（2）当销售单价定为9元/千克时，每天可获利润w最大
【解析】分析：（1）设购进荔枝a千克，荔枝售价定为b元/千克时，水果商要不亏本，由题意建立不等式求出其值就可以了．
（2）由（1）可知，每千克荔枝的平均成本为6元，再根据售价-进价=利润就可以表示出w，然后化为顶点式就可以求出最值．
本题解析：
（1）设购进荔枝a千克，...