题目内容
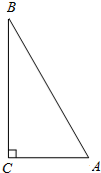 我们在学习“§2.5等腰三角形的轴对称性”时,有一个思考:“如图,在Rt△ABC中,∠ACB=90°,如果∠B=30°,那么AC与AB有怎样的数量关系?”请你写出AC与AB所满足的数量关系并证明.
我们在学习“§2.5等腰三角形的轴对称性”时,有一个思考:“如图,在Rt△ABC中,∠ACB=90°,如果∠B=30°,那么AC与AB有怎样的数量关系?”请你写出AC与AB所满足的数量关系并证明.考点:含30度角的直角三角形,等边三角形的判定与性质
专题:
分析:方法一:取AB的中点D,连接CD,根据直角三角形斜边上的中线等于斜边的一半可得DB=CD=AD,再根据直角三角形两锐角互余求出∠A=60°,然后判断出△ACD是等边三角形,根据等边三角形的性质可得AC=CD=AD,从而得证;
方法二:延长AC到D,使AC=DC,利用“边角边”证明△BCA和△BCD全等,根据全等三角形对应角相等可得∠ABC=∠DBC=30°,∠D=∠A=60°,然后判断出△ABD是等边三角形,AD=AB,再根据AD=2AC等量代换即可得证.
方法二:延长AC到D,使AC=DC,利用“边角边”证明△BCA和△BCD全等,根据全等三角形对应角相等可得∠ABC=∠DBC=30°,∠D=∠A=60°,然后判断出△ABD是等边三角形,AD=AB,再根据AD=2AC等量代换即可得证.
解答: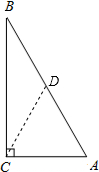 解:数量关系:AB=2AC.
解:数量关系:AB=2AC.
理由如下:方法一:取AB的中点D,连接CD,
∵∠ACB=90°,
∴DB=CD=AD,
又∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴AC=CD=AD,
∴AC=CD=AD=BD,
即AB=2AC;
方法二:证明:延长AC到D,使AC=DC,
∵∠ACB=90°,∠ABC=30°,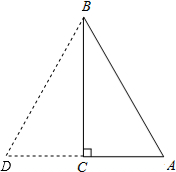
∴∠ACB=∠DCB=90°,∠A=60°,
在△BCA和△BCD中,
,
∴△BCA≌△BCD(SAS),
∴∠ABC=∠DBC=30°,∠D=∠A=60°,
即∠DBA=60°,
∴△ABD是等边三角形,AD=AB,
又∵AC=DC,
∴AD=2AC,
∴AB=2AC.
 解:数量关系:AB=2AC.
解:数量关系:AB=2AC.理由如下:方法一:取AB的中点D,连接CD,
∵∠ACB=90°,
∴DB=CD=AD,
又∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴AC=CD=AD,
∴AC=CD=AD=BD,
即AB=2AC;
方法二:证明:延长AC到D,使AC=DC,
∵∠ACB=90°,∠ABC=30°,

∴∠ACB=∠DCB=90°,∠A=60°,
在△BCA和△BCD中,
|
∴△BCA≌△BCD(SAS),
∴∠ABC=∠DBC=30°,∠D=∠A=60°,
即∠DBA=60°,
∴△ABD是等边三角形,AD=AB,
又∵AC=DC,
∴AD=2AC,
∴AB=2AC.
点评:本题考查了直角三角形30°角所对的直角边等于斜边的一半的证明,主要利用了等边三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,作辅助线构造出等边三角形是解题的关键.

练习册系列答案
相关题目
 如图,D是△ABC的AB边上一点,∠1=∠B,AD=3,BD=4,求AC的长度.
如图,D是△ABC的AB边上一点,∠1=∠B,AD=3,BD=4,求AC的长度. 面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.
面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.