题目内容
 面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.
面积为1的正方形ABCD中,F是BC的中点,BD、AF交于E点,求正方形被分成四部分的面积.考点:正方形的性质
专题:
分析:由于四边形ABCD是正方形,那么AD∥BC,AD=BC,根据平行线分线段成比例定理的推论可得△BEF∽△DAF,于是S△BEF:S△DAF=(
)2,E是BC中点可知BE:AD=1:2,根据三角形面积公式从而求得S△ABF=
S△ABD=
,S△ADF=
-
=
,S△BEF=
SDAF=
×
=
,S四边形DCEF=
-
=
.
| BE |
| AD |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 12 |
| 5 |
| 12 |
解答:解:∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,
∴△BEF∽△DAF,
∴BF:DF=BE:AD,S△BEF:S△DAF=(
)2,
∵E是BC中点,
∴BE=CE,
∴BE:AD=1:2,
∴S△ABF:S△ADF=1:2,S△BEF:S△DAF=1:4,
∵S△ABD=S△BCD=
S正方形=
∴S△ABF=
S△ABD=
×
=
,S△ADF=
-
=
,
∴S△BEF=
SDAF=
×
=
,
∴S四边形DCEF=
-
=
;
∴AD∥BC,AD=BC,
∴△BEF∽△DAF,
∴BF:DF=BE:AD,S△BEF:S△DAF=(
| BE |
| AD |
∵E是BC中点,
∴BE=CE,
∴BE:AD=1:2,
∴S△ABF:S△ADF=1:2,S△BEF:S△DAF=1:4,
∵S△ABD=S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABF=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
∴S△BEF=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
∴S四边形DCEF=
| 1 |
| 2 |
| 1 |
| 12 |
| 5 |
| 12 |
点评:本题考查了面积以及等积变换、相似三角形的判定和性质,解题的关键是找出四部分面积之间的关系.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
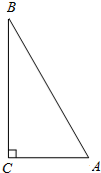 我们在学习“§2.5等腰三角形的轴对称性”时,有一个思考:“如图,在Rt△ABC中,∠ACB=90°,如果∠B=30°,那么AC与AB有怎样的数量关系?”请你写出AC与AB所满足的数量关系并证明.
我们在学习“§2.5等腰三角形的轴对称性”时,有一个思考:“如图,在Rt△ABC中,∠ACB=90°,如果∠B=30°,那么AC与AB有怎样的数量关系?”请你写出AC与AB所满足的数量关系并证明. 如图,有一圆柱体,它的高为8cm,底面周长为12cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是
如图,有一圆柱体,它的高为8cm,底面周长为12cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是