题目内容
已知△ABC中，CD⊥AB交AB于点D，BD=4，CD=2，AD=1，判断△ABC是否是直角三角形？
考点：勾股定理的逆定理
专题：
分析：根据勾股定理首先求出AC2、BC2、AB2，得到AB2=AC2+BC2，问题即可解决．
解答：
解：如图，△ABC是直角三角形．理由如下：
∵CD⊥AB交AB于点D，
∴由勾股定理得：
AC2=12+22=5，BC2=22+42=20；
而AB2=52=25，
∴AB2=AC2+BC2，
∴△ABC是直角三角形．
解：如图，△ABC是直角三角形．理由如下：∵CD⊥AB交AB于点D，
∴由勾股定理得：
AC2=12+22=5，BC2=22+42=20；
而AB2=52=25，
∴AB2=AC2+BC2，
∴△ABC是直角三角形．
点评：该题主要考查了勾股定理及其逆定理的应用问题；解题的关键是灵活运用勾股定理求出有关线段的长度；对灵活运用能力提出了一定的要求．
练习册系列答案
孟建平名校考卷系列答案
相关题目
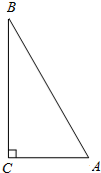我们在学习“§2.5等腰三角形的轴对称性”时，有一个思考：“如图，在Rt△ABC中，∠ACB=90°，如果∠B=30°，那么AC与AB有怎样的数量关系？”请你写出AC与AB所满足的数量关系并证明．
如图，在半径为10cm的圆中作一个正六边形ABCDEF，试求此正六边形的面积．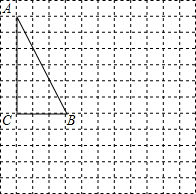
在下面的网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，BC=3，AC=6．