题目内容
16.计算:(1)(3$\sqrt{2}$-1)(1+3$\sqrt{2}$)-(3$\sqrt{2}$-1)2;
(2)$\frac{2}{3}$$\sqrt{9x}$-6$\sqrt{\frac{x}{4}}$-x$\sqrt{\frac{1}{x}}$.
分析 (1)利用平方差公式和完全平方公式计算;
(2)先把二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=18-1-(18-6$\sqrt{2}$+1)
=18-1-18+6$\sqrt{2}$-1、
=6$\sqrt{2}$-2;
(2)原式=2$\sqrt{x}$-3$\sqrt{x}$-$\sqrt{x}$
=-2$\sqrt{x}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
6.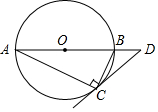 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
4. 如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )
如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )
 如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )
如图,DE是△ABC中AC边的垂直平分线,若BC=8,AB=10,则△EBC的周长是( )| A. | 13 | B. | 16 | C. | 18 | D. | 20 |
5. 如图所示,射线OP表示的方向是( )
如图所示,射线OP表示的方向是( )
 如图所示,射线OP表示的方向是( )
如图所示,射线OP表示的方向是( )| A. | 东偏北65° | B. | 北偏东25° | C. | 北偏西65° | D. | 北偏东65° |
6. 已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
 已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )| A. | m>0,n<3 | B. | m<0,n>3 | C. | m<0,n<3 | D. | m>0,n>3 |
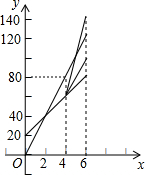 某部队甲、乙现两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.
某部队甲、乙现两班参加植树活动.乙班先植树20棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.