题目内容
6.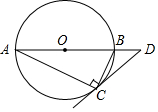 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 55° |
分析 连接OC,由圆周角定理可求得∠COD,由切线的性质可知∠OCD=90°,则可求得∠D.
解答  解:
解:
连接OC,
则∠COD=2∠A=50°,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∴∠D=90°∠COD=40°,
故选C.
点评 本题主要考切线的性质和圆周角定理,利用圆周角定理求得∠COD是解题的关键,注意有关切线问题中辅助线的运用.

练习册系列答案
相关题目
11.如图,点O是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使$\widehat{AB}$和$\widehat{BC}$都经过圆心O,已知⊙O的半径为3,则阴影部分的面积是( )
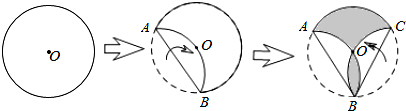

| A. | $\frac{9}{4}π$ | B. | $\frac{9}{2}π$ | C. | 2π | D. | 3π |
18.-2014的相反数是( )
| A. | $-\frac{1}{2014}$ | B. | $\frac{1}{2014}$ | C. | -2014 | D. | 2014 |
15.一个物体作上下方向的运动,规定向上运动5m记作+5m,那么向下运动5m记作( )
| A. | -5m | B. | 5m | C. | 10m | D. | -10m |