题目内容
2.下列计算正确的是( )| A. | $\sqrt{8}$+$\sqrt{2}$=$\sqrt{10}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{8}×\sqrt{2}$=$\sqrt{16}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=$\sqrt{4}$ |
分析 根据二次根式的加减法对A、B进行判断;根据二次根式的乘法法则对C进行判断;根据二次根式的除法法则对D进行判断.
解答 解:A、原式=2$\sqrt{2}$+$\sqrt{2}$=3$\sqrt{2}$,所以A选项错误;
B、原式=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,所以B选项正确;
C、原式=$\sqrt{8×2}$=$\sqrt{16}$=4,所以C选项错误;
D、原式=$\sqrt{8÷2}$=$\sqrt{4}$=2,所以D选项错误.
故选B.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.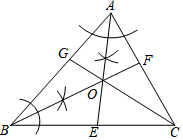 如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
 如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | CG也是△ABC的一条内角平分线 | ||
| C. | AO=BO=CO | D. | 点O到△ABC三边的距离相等 |
17.下列说法中,错误的是( )
| A. | 2是4的算术平方根 | B. | $\frac{1}{3}$是$\frac{1}{9}$的一个平方根 | ||
| C. | (-1)2的平方根是-1 | D. | 0的平方根是0 |
14.为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
(1)求a、b的值.
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
| 甲型 | 乙型 | |
| 价格(元/台) | a | b |
| 有效半径(米/台) | 150 | 100 |
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
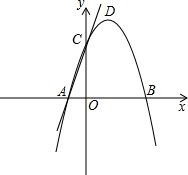 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.