题目内容
2.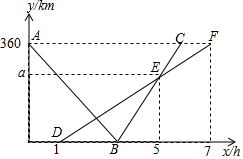 快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
分析 (1)根据速度=路程÷时间可求出慢车的速度,再根据路程=速度×时间可求出a值;
(2)根据路程=速度×时间(时间分段),可得出AB、BC、DF段的函数解析式,当AB、DF段的函数解析式y值相等时,可求出快车与慢车第一次相遇时距离佳市的路程;
(3)由当x=1时AB段的y值大于100和当x=6时DF段的y值小于100,可确定分1≤x≤3和3≤x≤6两种情况考虑,根据两车相距100km可列出关于x的含绝对值符号的一元一次方程,解之即可得出结论.
解答 解:(1)慢车的速度为360÷(7-1)=60(km/h),
a=60×(5-1)=240.
答:慢车的速度为60km/h,a的值为240.
(2)快车的速度为(360+240)÷5=120(km/h).
根据题意得:AB段的解析式为y=360-120x(0≤x≤3);
BC段的解析式为y=120(x-3)=120x-360(3≤x≤6);
DF段的解析式为y=60(x-1)=60x-60(1≤x≤7).
当y=360-120x=60x-60时,x=$\frac{7}{3}$,
此时y=60x-60=60×$\frac{7}{3}$-60=80.
答:快车与慢车第一次相遇时,距离佳市的路程是80千米.
(3)当x=1时,y=360-120x=240>100,
当x=6时,y=60x-60=300,360-300=60<100,
∴分1≤x≤3和3≤x≤6两种情况考虑.
当1≤x≤3时,有|360-120x-(60x-60)|=100,
解得:x1=$\frac{16}{9}$,x2=$\frac{26}{9}$;
当3≤x≤6时,有|60x-60-(120x-360)|=100,
解得:x3=$\frac{16}{3}$,x4=$\frac{26}{3}$(舍去).
综上所述:快车出发$\frac{16}{9}$、$\frac{26}{9}$或$\frac{16}{3}$小时后两车相距为100km.
点评 本题考查了一次函数的应用以及解含绝对值符号的一元一次方程,解题的关键是:(1)根据数量关系,列式计算;(2)根据数量关系,找出AB、BC、DF段的函数解析式;(3)分1≤x≤3和3≤x≤6两种情况,列出关于x的含绝对值符号的一元一次方程.

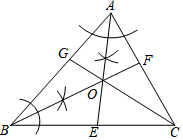 如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )
如图,AE与BF交于点O,点O在CG上,根据尺规作图的痕迹,判断下列说法不正确的是( )| A. | AE、BF是△ABC的内角平分线 | B. | CG也是△ABC的一条内角平分线 | ||
| C. | AO=BO=CO | D. | 点O到△ABC三边的距离相等 |
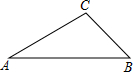 已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.
已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.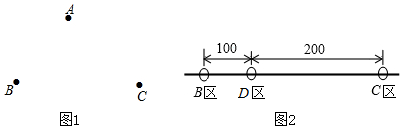
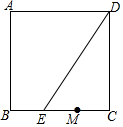 如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.
如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.
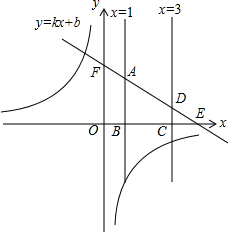 已知反比例函数y=$\frac{k}{x}$的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F
已知反比例函数y=$\frac{k}{x}$的图象在第二、四象限,一次函数为y=kx+b(b>0),直线x=1与x轴交于点B,与直线y=kx+b交于点A,直线x=3与x轴交于点C,与直线y=kx+b交于点D.点A,D都在第一象限,直线y=kx+b与x轴交于点E,与y轴交于点F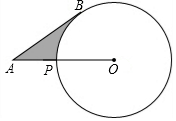 如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2
如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5cm,AB=5$\sqrt{3}$cm,则劣弧$\widehat{BP}$与AB,AP所围成的阴影的面积是($\frac{25}{2}\sqrt{3}-\frac{25π}{6}$)cm2