题目内容
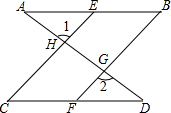 如图,直线AD与AB,CD相交于A,D,两点,EC,BF,与AB、CD相交于点E,C,B,F,如果∠1=∠2,∠B=∠C.小明在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF,同桌的小慧说:“不光有这个发现,我还能得到∠A=∠D呢.”小明在深入其中,很快也明白了小慧是怎样得到∠A=∠D的了.你能帮助他们写出过程吗?
如图,直线AD与AB,CD相交于A,D,两点,EC,BF,与AB、CD相交于点E,C,B,F,如果∠1=∠2,∠B=∠C.小明在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF,同桌的小慧说:“不光有这个发现,我还能得到∠A=∠D呢.”小明在深入其中,很快也明白了小慧是怎样得到∠A=∠D的了.你能帮助他们写出过程吗?考点:平行线的判定与性质
专题:
分析:由条件可先证明BF∥CE,再证明AB∥CD,可得到∠A=∠D.
解答:证明:
∵∠1=∠CHD,且∠1=∠2,
∴∠2=∠CHD,
∴BF∥CE,
∴∠C=∠BFD,
又∠C=∠B,
∴∠B=∠BFD,
∴AB∥CD,
∴∠A=∠D.
∵∠1=∠CHD,且∠1=∠2,
∴∠2=∠CHD,
∴BF∥CE,
∴∠C=∠BFD,
又∠C=∠B,
∴∠B=∠BFD,
∴AB∥CD,
∴∠A=∠D.
点评:本题主要考查平行线的性质和判定,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知正比例函数y=(3m+1)x的图象上有两点A(x1,y1)、B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A、m<-
| ||
B、m>-
| ||
| C、m<0 | ||
| D、m>0 |
 如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=
如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=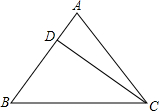 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm, 如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC=
如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC= 如图,∠1=∠3,∠B=∠C,试说明∠A=∠D的理由.
如图,∠1=∠3,∠B=∠C,试说明∠A=∠D的理由. 如图,已知∠1=∠2,∠BAD=∠BCD,证明:AD∥BC.
如图,已知∠1=∠2,∠BAD=∠BCD,证明:AD∥BC. 如图,已知AB∥CD,∠1=35°,BD平分∠ADC,求∠A的度数.
如图,已知AB∥CD,∠1=35°,BD平分∠ADC,求∠A的度数.