题目内容
 如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )
如图是一圆锥的侧面展开图,其弧长为10π,则该圆锥的全面积为 ( )| A、60π | B、85π |
| C、95π | D、169π |
考点:圆锥的计算,弧长的计算
专题:计算题
分析:设圆锥的底面圆的半径为r,扇形的半径为R,先根据弧长公式得到
=10π,解得R=12,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到
2π•r=10π,解得r=5,然后计算底面积与侧面积的和.
| 150•π•R |
| 180 |
2π•r=10π,解得r=5,然后计算底面积与侧面积的和.
解答:解:设圆锥的底面圆的半径为r,扇形的半径为R,
根据题意得
=10π,解得R=12,
2π•r=10π,解得r=5,
所以该圆锥的全面积=π•52+
•10π•12=85π.
故选B.
根据题意得
| 150•π•R |
| 180 |
2π•r=10π,解得r=5,
所以该圆锥的全面积=π•52+
| 1 |
| 2 |
故选B.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
 如图,直线AB分别交x轴,y轴于点A,B,
如图,直线AB分别交x轴,y轴于点A,B,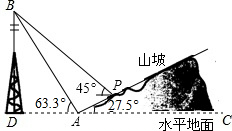 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)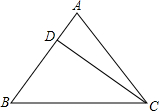 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm, 如图直角坐标系中,A(-3,2),B(4,6),线段AB与y轴交于C点.
如图直角坐标系中,A(-3,2),B(4,6),线段AB与y轴交于C点. 如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC=
如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC= 如图,∠1=∠3,∠B=∠C,试说明∠A=∠D的理由.
如图,∠1=∠3,∠B=∠C,试说明∠A=∠D的理由. 已知:如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且ED∥AC,FD∥AB,AB=9.求证:四边形AEDF是平行四边形.
已知:如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且ED∥AC,FD∥AB,AB=9.求证:四边形AEDF是平行四边形.