题目内容
17.已知,在△ABC中,∠A-∠B=30°,∠A+∠B=2∠C,求∠A的度数.分析 由已知∠A-∠B=30°,∠A+∠B=2∠C,和三角形内角和∠A+∠B+∠C=180°,解方程组即可求出结论.
解答 解:由∠A-∠B=30°,∠A+∠B=2∠C,
得∠A=15°+∠C,∠B=∠C-15°
在△ABC中,∠A+∠B+∠C=180°,
∴15°+∠C+∠C-15°+∠C=180°,
∴∠C=60°,
∴∠A=75°.
点评 本题考查了三角形内角和定理的应用,注意:三角形的内角和等于180°和方程思想的应用.

练习册系列答案
相关题目
2.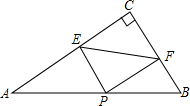 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )| A. | 5 | B. | $\frac{3}{2}$ | C. | 4 | D. | $\frac{24}{5}$ |
7.判定两个等腰三角形全等的条件可以是( )
| A. | 有一腰和一角对应相等 | B. | 有两角一边对应相等 | ||
| C. | 有顶角和一个底角对应相等 | D. | 有两角对应相等 |
 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是a.
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是a.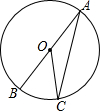 如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=20°.
如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=20°.