题目内容
1.代数式2x2+3y2-8x+6y+1的最小值是-10.分析 把代数式2x2+3y2-8x+6y+1根据完全平方公式化成几个完全平方和的形式,再进行求解.
解答 解:2x2+3y2-8x+6y+1
=2(x-2)2+3(y+1)2-10.
∵2(x-2)2≥0,3(y+1)2≥0,
∴代数式2x2+3y2-8x+6y+1的最小值是-10.
故答案是:-10.
点评 本题考查了配方法的应用.解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13. 如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )
如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )
 如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )
如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )| A. | 5+$\sqrt{2}$+$\sqrt{7}$ | B. | 5+$\sqrt{2}$+$\sqrt{13}$ | C. | $\sqrt{2}$+$\sqrt{13}$+$\sqrt{17}$ | D. | $\sqrt{2}$+$\sqrt{58}$ |
11.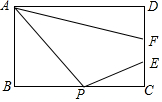 如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
 如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )
如图,在矩形ABCD中,AB=6,AD=8,点P是BC中点,点E、F是边CD上的任意两点,且EF=2,当四边形APEF的周长最小时,则DF的长为( )| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
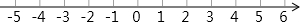
 如图,从A地到B地共有五条路,你应选择第③条路(填标出的数字),因为两点之间线段最短.
如图,从A地到B地共有五条路,你应选择第③条路(填标出的数字),因为两点之间线段最短.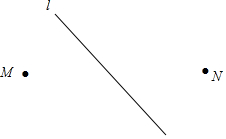 2016年7月31日下午,张家口和北京延庆区同时举办“纪念申冬奥成功一周年活动”,并在该活动上表明,张家口要筹划建成一个以崇礼为核心、周边的赤城、张北等为补充的集中连片滑雪大区,形成能让1000万人同时滑雪的区域.如图,规划人员计划在高速公路l旁的大片空地建设M和N两个滑雪场,同时还要建设两条道路使得滑雪场M和N各自到高速公路l的距离都最近,请你帮规划人员设计出这两条道路.
2016年7月31日下午,张家口和北京延庆区同时举办“纪念申冬奥成功一周年活动”,并在该活动上表明,张家口要筹划建成一个以崇礼为核心、周边的赤城、张北等为补充的集中连片滑雪大区,形成能让1000万人同时滑雪的区域.如图,规划人员计划在高速公路l旁的大片空地建设M和N两个滑雪场,同时还要建设两条道路使得滑雪场M和N各自到高速公路l的距离都最近,请你帮规划人员设计出这两条道路.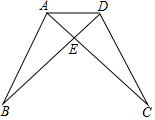 从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:①②(只填序号)
从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).已知:①②(只填序号)