题目内容
13. 如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )
如图.抛物线y=-x2+2x+3交x轴于点A(a,0),B(b,0),交y轴于点C,抛物线的顶点为D,点C关于抛物线对称轴的对称点为E,点G、F分别在x轴、y轴上,则四边形EDFG的周长的最小值为( )| A. | 5+$\sqrt{2}$+$\sqrt{7}$ | B. | 5+$\sqrt{2}$+$\sqrt{13}$ | C. | $\sqrt{2}$+$\sqrt{13}$+$\sqrt{17}$ | D. | $\sqrt{2}$+$\sqrt{58}$ |
分析 根据抛物线解析式求得点D(1,4)、点E(2,3),作点D关于y轴的对称点D′(-1,4)、作点E关于x轴的对称点E′(2,-3),从而得四边形EDFG的周长=DE+DF+FG+GE=DE+D′F+FG+GE′,当点D′、F、G、E′四点共线时,周长最短,据此根据两点间的距离公式可得答案.
解答 解:如图,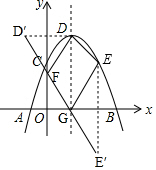
在y=-x2+2x+3中,当x=0时,y=3,即点C(0,3),
∵y=-x2+2x+3=-(x-1)2+4,
∴对称轴为x=1,顶点D(1,4),
则点C关于对称轴的对称点E的坐标为(2,3),
作点D关于y轴的对称点D′(-1,4),作点E关于x轴的对称点E′(2,-3),
连接D′、E′,D′E′与x轴的交点G、与y轴的交点F即为使四边形EDFG的周长最小的点,
四边形EDFG的周长=DE+DF+FG+GE
=DE+D′F+FG+GE′
=DE+D′E′
=$\sqrt{(1-2)^{2}+(4-3)^{2}}$+$\sqrt{(-1-2)^{2}+(4+3)^{2}}$
=$\sqrt{2}$+$\sqrt{58}$,
∴四边形EDFG的周长的最小值为$\sqrt{2}$+$\sqrt{58}$,
故选:D.
点评 本题主要考查抛物线与x轴的交点、轴对称-最短路线问题,根据轴对称的性质得出点F、G的位置是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 建筑工人在砌墙时,经常在两个墙角分别立一根标志杆,在两根标志杆之间拉一条线,沿这条线就可以砌出直的墙了,其中的数学道理是两点确定一条直线.
建筑工人在砌墙时,经常在两个墙角分别立一根标志杆,在两根标志杆之间拉一条线,沿这条线就可以砌出直的墙了,其中的数学道理是两点确定一条直线.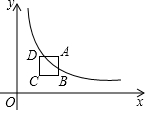 在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图1,若双曲线y=$\frac{5}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{5}$≤a≤$\sqrt{5}$+1.
在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图1,若双曲线y=$\frac{5}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{5}$≤a≤$\sqrt{5}$+1.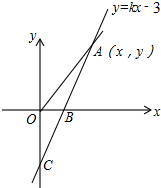 如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB