题目内容
9．求出下列函数中自变量x的取值范围．①y=$\frac{1}{x-2}$
②y=$\sqrt{2+x}$．
分析 （1）根据分式的分母不为零分式有意义，可得答案；
（2）根据二次根式的被开方数是非负数，可得答案．
解答 解：（1）由y=$\frac{1}{x-2}$有意义，得x-2≠0，
解得x≠2；
（2）由y=$\sqrt{2+x}$有意义，得
x+2≥0，
解得x≥-2．
点评 本题考查了函数自变量的范围，当函数表达式是整式时，自变量可取全体实数；当函数表达式是分式时，考虑分式的分母不能为0；当函数表达式是二次根式时，被开方数非负．
练习册系列答案
相关题目
17．下列运算正确的是（ ）
| A． | -$\frac{5}{7}$+$\frac{2}{7}$=-（$\frac{5}{7}$+$\frac{2}{7}$）=-1 | B． | -7-2×5=-9×5=-45 | ||
| C． | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | D． | |3-5|=-（3-5） |
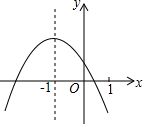如图是抛物线y=ax2+bx+c的图象，则下列说法正确的有（ ）个．