题目内容
1.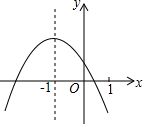 如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.
如图是抛物线y=ax2+bx+c的图象,则下列说法正确的有( )个.①a<0;②b>0;③c>0;④abc>0;⑤a-b+c>0;⑥a+b+c>0;⑦2a-b<0.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴的符号进行推理,进而对所得结论进行判断.
解答 解:①∵根据图示知,二次函数图象的开口方向向下,
∴a<0;
故本选项正确;
②∵对称轴x=-$\frac{b}{2a}$<0,
∴b<0;
故本选项错误;
③∵该函数图象与y轴交于正半轴,
∴c>0;
故本选项正确;
④a<0,b<0,c>0,
abc>0,
故本选项正确;
⑤∵当x=-1时,
∴y>0,即a-b+c>0;
故本选项正确;
⑥当x=1时,y<0,即a+b+c<0;
故本选项错误;
⑦∵-$\frac{b}{2a}$>-1,
∴2a-b>0,
故本选项错误;
综上所述,以上说法中正确的有①③④⑤,共4个.
故选:A.
点评 此题考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
6.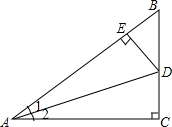 如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )| A. | BD=DF | B. | DE=DC | C. | BE=CF | D. | AE=AC |

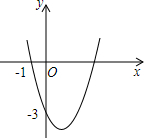 如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限.设m=a+b+c,则m的取值范围是-6<m<0.
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限.设m=a+b+c,则m的取值范围是-6<m<0. 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形的数字表示在该位置的小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.