题目内容
14.根据所给的条件,求出各式的值:(1)若|a-3|与(b-2)2互为相反数,求(-a)b的值.
(2)已知:|a|=3,|b|=2,且ab<0,求a-b的值.
分析 (1)根据非负数的性质列出算式,求出a、b的值,计算即可;
(2)根据绝对值的性质和有理数的乘法法则解答.
解答 解:(1)由题意得,|a-3|+(b-2)2,=0,
则a-3=0,b-2=0,
解得,a=3,b=2,
则(-a)b=9;
(2)∵|a|=3,
∴a=±3,
∵|b|=2,
∴b=±2,
∵ab<0,
∴a=3,b=-2,则a-b=5,
a=-3,b=2,则a-b=-5.
点评 本题考查的是非负数的性质和绝对值的性质,掌握有限个非负数的和为零,那么每一个加数也必为零是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
2.△ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )
| A. | 35cm | B. | 30cm | C. | 45cm | D. | 55cm |
6.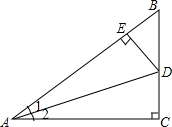 如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
 如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )
如图,在Rt△ABC中,∠C=90°,∠1=∠2,DE⊥AB,下列结论中,正确的是( )| A. | BD=DF | B. | DE=DC | C. | BE=CF | D. | AE=AC |
 如图是由6个相同的小正方体搭成的几何体,那么这个几何体从左边看到的形状图是( )
如图是由6个相同的小正方体搭成的几何体,那么这个几何体从左边看到的形状图是( )


