题目内容
18．二次函数y=x2+kx+1与y=x2+x+k有相同的最小值，则k=1或-5．分析 利用顶点坐标公式求得顶点纵坐标，建立关于k的方程得出答案即可．
解答 解：∵二次函数y=x2+kx+1的最小值为$\frac{4-{k}^{2}}{4}$，y=x2+x+k的最小值是$\frac{4k-1}{4}$，最小值相同，
∴$\frac{4-{k}^{2}}{4}$=$\frac{4k-1}{4}$，
解得：k=1或-5．
故答案为：1或-5．
点评 本题考查了二次函数的最值：二次函数y=ax2+bx+c（a≠0），当a＞0时，抛物线在对称轴左侧，y随x的增大而减少；在对称轴右侧，y随x的增大而增大，因为图象有最低点，所以函数有最小值，当x=-$\frac{b}{2a}$时，y=$\frac{4ac-{b}^{2}}{4a}$；当a＜0时，抛物线在对称轴左侧，y随x的增大而增大；在对称轴右侧，y随x的增大而减少，因为图象有最高点，所以函数有最大值，当x=-$\frac{b}{2a}$时，y=$\frac{4ac-{b}^{2}}{4a}$．
练习册系列答案
阅读快车系列答案
相关题目
根据图填空：（1）a＞0； （2）b＜0；（3）c＞0；（4）b2-4ac＞0．
6．
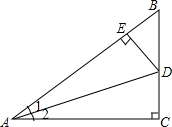如图，在Rt△ABC中，∠C=90°，∠1=∠2，DE⊥AB，下列结论中，正确的是（ ）
如图，在Rt△ABC中，∠C=90°，∠1=∠2，DE⊥AB，下列结论中，正确的是（ ）| A． | BD=DF | B． | DE=DC | C． | BE=CF | D． | AE=AC |
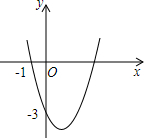如图，抛物线y=ax2+bx+c（a≠0）过点（-1，0）和点（0，-3），且顶点在第四象限．设m=a+b+c，则m的取值范围是-6＜m＜0．