题目内容
18.适合下列条件的△ABC中,直角三角形的个数为③④.①a=$\frac{1}{3},b=\frac{1}{4},c=\frac{1}{5}$;②a=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25;⑤a=2,b=2,c=4.
分析 根据勾股定理的逆定理及直角三角形的性质对各小题进行逐一分析即可.
解答 解:①∵b2+c2=($\frac{1}{4}$)2+($\frac{1}{5}$)2≠c2,∴△ABC不是直角三角形,故本小题错误;
②不能判定△ABC的形状,故本小题错误;
③∵∠A=32°,∠B=58°,∴∠C=180°-32°-58°=90°,∴△ABC是直角三角形,故本小题正确;
④∵a2+b2=72+242=625≠c2,∴△ABC是直角三角形,故本小题正确;
⑤∵b2+a2=22+22=8≠c2=16,∴△ABC不是直角三角形,故本小题错误.
故答案为:③④.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
10.下列计算中正确的是( )
| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | $\sqrt{4}$+$\sqrt{4}$=4 |
8.三角形A′B′C′是由三角形ABC平移得到的,点A(-1,-4)的对应点为A′(1,-1),则点B(1,1)的对应点B′、点C(-1,4)的对应点C′的坐标分别为( )
| A. | (2,2)(3,4) | B. | (3,4)(1,7) | C. | (-2,2)(1,7) | D. | (3,4)(2,-2) |
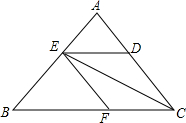 如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.
如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.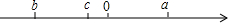 已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.
已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.