题目内容
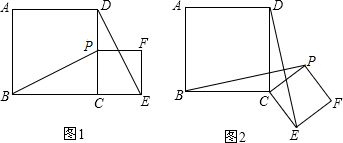
8. 如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.
如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.
分析 根据DE∥BC,EF∥AC,得到四边形EFCD是平行四边形,由于CE是△ABC的角平分线,得到∠DEC=∠FCE,等量代换得到∠DEC=∠DCE,于是得到DE=DC,证得四边形EFCD是菱形,于是得到结论.
解答 证明:∵DE∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∵CE是△ABC的角平分线,
∴∠DEC=∠FCE,
∴∠DEC=∠DCE,
∴DE=DC,
∴四边形EFCD是菱形,
∴CE是∠DEF的平分线.
点评 本题考查了平行四边形的判定与性质、平行线的性质、等腰三角形的判定与性质;证明平行四边形和等腰三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.实数a、b满足(a+b)2+a+b=0,则(a+b)2的值为( )
| A. | 4 | B. | 1 | C. | -2或1 | D. | 4或1 |
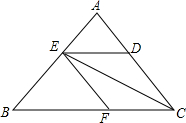
 如图所示已知,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P的度数.
如图所示已知,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P的度数.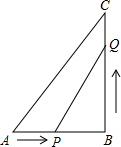 在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.
在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.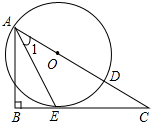 如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 如图,△ACB是等腰直角三角形,∠ACB=90°,△EFG是以A点为中心的等边三角形,P为△EFG边上的任意一点,连结CP,把CP绕点C顺时针旋转90°到CQ的位置.
如图,△ACB是等腰直角三角形,∠ACB=90°,△EFG是以A点为中心的等边三角形,P为△EFG边上的任意一点,连结CP,把CP绕点C顺时针旋转90°到CQ的位置.