题目内容
15.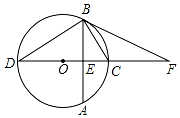 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;(1)求证:∠CBF=∠CDB.
(2)若AB=8,CE=2,求⊙O的直径.
分析 (1)连接OB,由切线的性质和圆周角定理可求得∠OBF=∠CBD=90°,再利用角的和差可求得∠CBF=∠OBD,再由圆的性质可求得∠CDB=∠OBD,可证得结论;
(2)可设半径为r,则OE=r-2,由垂径定理可求得BE=4,在Rt△OBE中,由勾股定理可列方程,可求得r,则可求得⊙O的直径.
解答 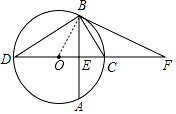 (1)证明:
(1)证明:
如图,连接OB,
∵FB为⊙O的切线,
∴OB⊥BF,即∠OBF=90°,
∵CD为直径,
∴∠CBD=90°,
∴∠CBF+∠OBC=∠OBC+∠DBO=90°,
∴∠CBF=∠DBO,
∵OB=OD,
∴∠CDB=∠DBO,
∴∠CBF=∠CDB;
(2)解:
设⊙O的半径为r,则OE=OC-CE=r-2,
∵AB⊥CD,且CD为直径,
∴BE=$\frac{1}{2}$AB=4,
在Rt△OBE中,由勾股定理可得OB2=OE2+BE2,
∴r2=(r-2)2+42,解得r=5,
∴⊙O的直径为10.
点评 本题主要考查切线的性质及垂径定理,在(1)中利用切线的性质和圆周角定理求得∠OBD=∠CBF是解题的关键,在(2)中注意方程思想的应用.

练习册系列答案
相关题目
6.若点(m,n)在函数y=2x-1的图象上,则2m-n的值是( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
10.如图,10×2网格中有一个△ABC,图中与△ABC相似的三角形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图所示,正三棱柱的俯视图是( )
如图所示,正三棱柱的俯视图是( )
 如图所示,正三棱柱的俯视图是( )
如图所示,正三棱柱的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.若|x+y-5|+(x-y-3)2=0,则x2-y2的结果是( )
| A. | 2 | B. | 8 | C. | 15 | D. | 16 |