题目内容
7.如图,在平面直角坐标系中,二次函数y=-x2+2x+c的图象与x轴分别交于A、B两点,其中点B在点A的右侧,点A的坐标(-1,0),抛物线与y轴交于点C.(1)求二次函数解析式;
(2)P是抛物线上一动点,过P作y轴平行线,交直线BC于点E,设点P的横坐标为t,线段PE的长度为d(d≠0),求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,将射线PE绕点P顺时针旋转45°,交抛物线于点Q,当PQ:PE=2$\sqrt{2}$:3时,求t的值.
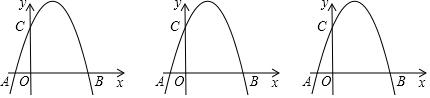
分析 (1)利用待定系数法,把点A坐标代入抛物线的解析式解方程即可.
(2)首先求出直线BC的解析式,设P(t,-t2+2t+3),则E(t,-t+3),分三种情形①当t<0时,d=-t+3-(-t2+2t+3)=t2-3t.②0<t<3时,d=-t2+2t+3-(-t+3)=-t2+3t.
③t>3时,d=-t+3-(-t2+2t+3)=t2-3t.分别求解即可.
(3)分两种情形讨论)①如图1中,当t<0时,由题意PQ=$\frac{2}{3}$$\sqrt{2}$PE=$\frac{2}{3}$$\sqrt{2}$(t2-3t),想办法用t表示Q点坐标,利用待定系数法即可解决问题.②如图2中,当0<t<3时,方法类似①.
解答 解:(1)把A(-1,0)代入y=-x2+2x+c得0=-1-2+c,
∴c=3,
∴二次函数的解析式为y=-x2+2x+3.
(2)对于抛物线y=-x2+2x+3,令y=0,得-x2+2x+3=0,解得x=-1或3,
∴A(-1,0),B(3,0),C(0,3),
∴直线BC的解析式为y=-x+3,
设P(t,-t2+2t+3),则E(t,-t+3),
①当t<0时,d=-t+3-(-t2+2t+3)=t2-3t.
②0<t<3时,d=-t2+2t+3-(-t+3)=-t2+3t.
③t>3时,d=-t+3-(-t2+2t+3)=t2-3t.
(3)①如图1中,当t<0时,由题意PQ=$\frac{2}{3}$$\sqrt{2}$PE=$\frac{2}{3}$$\sqrt{2}$(t2-3t),
∵∠EPQ=45°,P(t,-t2+2t+3),
∴点Q是横坐标为t+$\frac{2}{3}$(t2-3t)=$\frac{2}{3}$t2-t,点Q的纵坐标为-t2+2t+3+$\frac{2}{3}$(t2-3t)=-$\frac{1}{3}$t2+3,
∴Q($\frac{2}{3}$t2-t,-$\frac{1}{3}$t2+3),
把点Q坐标代入y=-x2+2x+3,得-$\frac{1}{3}$t2+3=-($\frac{2}{3}$t2-t)2+2($\frac{2}{3}$t2-t)+3,
整理得2t3-6t2-3t+9=0,
∴2t2(t-3)-3(t-3)=0,
∴(t-3)(2t2-3)=0,
∴t=-$\frac{\sqrt{6}}{2}$或$\frac{\sqrt{6}}{2}$或3,
∵t<0,
∴t=-$\frac{\sqrt{6}}{2}$.
②如图2中,当0<t<3时,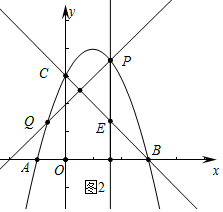
同法可得Q($\frac{2}{3}$t2-t,-$\frac{1}{3}$t2+3),
把点Q坐标代入y=-x2+2x+3,得-$\frac{1}{3}$t2+3=-($\frac{2}{3}$t2-t)2+2($\frac{2}{3}$t2-t)+3,
整理得2t3-6t2-3t+9=0,
∴2t2(t-3)-3(t-3)=0,
∴(t-3)(2t2-3)=0,
∴t=-$\frac{\sqrt{6}}{2}$或$\frac{\sqrt{6}}{2}$或3,
∵0<t<3,
∴t=$\frac{\sqrt{6}}{2}$.
③当t>3时,射线PQ与抛物线没有交点.
综上所述,在(2)的条件下,将射线PE绕点P顺时针旋转45°,交抛物线于点Q,当PQ:PE=2$\sqrt{2}$:3时,t=±$\frac{\sqrt{6}}{2}$.
点评 本题考查二次函数综合题、一次函数的应用、待定系数法等知识,解题的关键是灵活运用待定系数法,学会用分类讨论的思想思考问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x1<x2 | B. | x1>x2 | C. | x1=x2 | D. | 无法确定 |
| A. | 如果a2=b2,那么|a|=|b| | B. | 内错角相等 | ||
| C. | 周长相等的两个三角形全等 | D. | 若a>b,则ac2>bc2 |




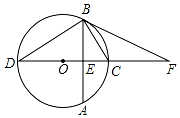 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且FB为⊙O的切线;