题目内容
1.下列各点,在函数y=-$\frac{1}{2}$x的图象上的是( )| A. | (1,2) | B. | (2,1) | C. | (1,-2) | D. | (-2,1) |
分析 分别将x=1、2、-2代入函数y=-$\frac{1}{2}$x求出y值,再对比四个选项中的点的坐标即可得出结论.
解答 解:当x=1时,y=-$\frac{1}{2}$x=-$\frac{1}{2}$,
∴A、C选项中的点均不在函数y=-$\frac{1}{2}$x的图象上;
当x=2时,y=-$\frac{1}{2}$x=-1,
∴B、选项中的点不在函数y=-$\frac{1}{2}$x的图象上;
当x=-2时,y=-$\frac{1}{2}$x=1,
∴D、选项中的点在函数y=-$\frac{1}{2}$x的图象上.
故选D.
点评 本题考查了一次函数图象上点的坐标特征,逐一分析四个选项中点是否在一次函数图象上是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
11.下列说法:
①一个无理数的相反数一定是无理数;
②一切实数都可以进行开立方运算,只有非负数才能进行开平方运算;
③一个有理数与一个无理数的和或差一定是无理数;
④实数m的倒数是$\frac{1}{m}$.
其中,正确的说法有( )
①一个无理数的相反数一定是无理数;
②一切实数都可以进行开立方运算,只有非负数才能进行开平方运算;
③一个有理数与一个无理数的和或差一定是无理数;
④实数m的倒数是$\frac{1}{m}$.
其中,正确的说法有( )
| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ①②③④ |
13.5的倒数是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
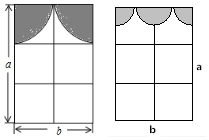 如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
 如图,在矩形ABCD中,AB=6,BC=8,G为AD中点,若E为AB边上一动点,当△CGE的周长为最小值时,则AE的长为2.
如图,在矩形ABCD中,AB=6,BC=8,G为AD中点,若E为AB边上一动点,当△CGE的周长为最小值时,则AE的长为2.