题目内容
13.设 x、y 是有理数,且 x,y 满足等式x2+2y+$\sqrt{2}$y=17-4$\sqrt{2}$,求x-y的值.分析 根据题意可以求得x、y的值,从而可以求得x-y的值.
解答 解:∵x、y 是有理数,且 x,y 满足等式x2+2y+$\sqrt{2}$y=17-4$\sqrt{2}$,
∴$\left\{\begin{array}{l}{{x}^{2}+2y=17}\\{y=-4}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=-4}\end{array}\right.$,
∴当x=5,y=-4时,x-y=5-(-4)=9,
当x=-5,y=-4时,原式=-5-(-4)=-1.
点评 本题考查实数,解答本题的关键是明确题意,求出相应的x、y的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若a、b、c为△ABC的三边长,且满足|a-4|+(b-2)2=0,则c的值可以为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
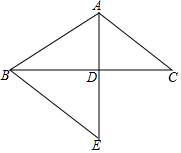 如图,△ABC中,AB=AC,线段BC的垂直平分线AD交BC于点D,过点BE作BE∥AC,交AD的延长线于点E,求证:AB=BE.
如图,△ABC中,AB=AC,线段BC的垂直平分线AD交BC于点D,过点BE作BE∥AC,交AD的延长线于点E,求证:AB=BE.