题目内容
9.计算及简化:(1)($\sqrt{a}$+$\frac{1}{\sqrt{a}}$)2-($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2
(2)$\frac{a-b}{\sqrt{a}-\sqrt{b}}$-$\frac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$.
分析 (1)根据完全平方公式可以解答本题;
(2)根据完全平方公式和平方差公式可以解答本题.
解答 解:(1)($\sqrt{a}$+$\frac{1}{\sqrt{a}}$)2-($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2
=$a+2+\frac{1}{a}-(a-2+\frac{1}{a})$
=$a+2+\frac{1}{a}-a+2-\frac{1}{a}$
=4;
(2)$\frac{a-b}{\sqrt{a}-\sqrt{b}}$-$\frac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$
=$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}-\sqrt{b}}$-$\frac{(\sqrt{a}-\sqrt{b})^{2}}{\sqrt{a}-\sqrt{b}}$
=$\sqrt{a}+\sqrt{b}-\sqrt{a}+\sqrt{b}$
=2$\sqrt{b}$.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图是某商场2012年至2016年销售额每年比上一年增长率的统计图,则这5年中,该商场销售额最大的是2016年.
如图是某商场2012年至2016年销售额每年比上一年增长率的统计图,则这5年中,该商场销售额最大的是2016年.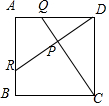 图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.
图中ABCD为正方形,Q及R分别为AD及AB上的点,DR与CQ相交于P,已知AQ=BR.