题目内容
5.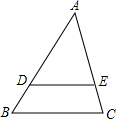 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,BC=6.(1)求DE的长;
(2)过点D作DF∥AC交BC于F,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求向量$\overrightarrow{DF}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示)
分析 (1)由$\frac{AD}{AB}$=$\frac{3}{4}$,AE=3,CE=1,可得$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{3}{4}$,即可证得DE∥BC,然后由平行线分线段成比例定理,即可求得DE的长;
(2)由DF∥AC,可得$\frac{DF}{AC}$=$\frac{BD}{BA}$=$\frac{1}{4}$,再由三角形法则,即可求得答案.
解答 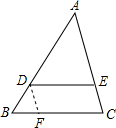 解:(1)∵AE=3,CE=1,
解:(1)∵AE=3,CE=1,
∴AC=AE+CE=4,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{3}{4}$,
∴DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{3}{4}$,
∴DE=BC×$\frac{3}{4}$=6×$\frac{3}{4}$=$\frac{9}{2}$;
(2)∵DF∥AC,
∴$\frac{DF}{AC}$=$\frac{BD}{BA}$=$\frac{1}{4}$,
∴$\overrightarrow{DF}$=$\frac{1}{4}$$\overrightarrow{AC}$=$\frac{1}{4}$($\overrightarrow{AB}$+$\overrightarrow{BC}$)=$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$.
点评 此题考查了平行向量的知识以及平行线分线段成比例定理.注意掌握三角形法则以及平行四边形的法则的应用是解此题的关键.

练习册系列答案
相关题目
20.多项式2xy-3xy2+25的次数及最高次项的系数分别是( )
| A. | 3,-3 | B. | 2,-3 | C. | 5,-3 | D. | 2,3 |
 如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b.
如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b. 将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.
将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形. 如图是由五个小正方体组成的立体图形,则从左面看到的平面图形是( )
如图是由五个小正方体组成的立体图形,则从左面看到的平面图形是( )



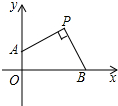 如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4.
如图,已知P(2,2),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=4. 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.