题目内容
11.当a<1时,化简$\sqrt{{-a}^{3}(1-a)}$的结果是-a$\sqrt{{a}^{2}-a}$.分析 根据二次根式的性质,可得答案.
解答 解:当a<1时,化简$\sqrt{{-a}^{3}(1-a)}$,得
a≤0,
化简$\sqrt{{-a}^{3}(1-a)}$的结果是-a$\sqrt{{a}^{2}-a}$,
故答案为:-a$\sqrt{{a}^{2}-a}$.
点评 本题考查了二次根式的性质与化简,利用了二次根式的性质:$\sqrt{{a}^{2}}$=a (a≥0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下面不可以判断四边形是平行四边形的是( )
| A. | 两组对边相等的四边形 | |
| B. | 两组对角相等的四边形 | |
| C. | 一组对边平行,一组邻角互补的四边形 | |
| D. | 一组对边平行,一组对角相等的四边形 |
19.方程$\frac{1}{1+x}$=$\frac{2}{1-{x}^{2}}$+1的解为( )
| A. | 0 | B. | -1 | C. | 2 | D. | -1或2 |
16.矩形具有而菱形不具有的性质是( )
| A. | 对角线相等 | B. | 两组对边分别平行 | ||
| C. | 对角线互相平分 | D. | 两组对角分别相等 |
3.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{\frac{x+9}{2}+1≥\frac{x+1}{3}-1}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a>-36 | B. | a≥-36 | C. | a<-36 | D. | a≤-36 |
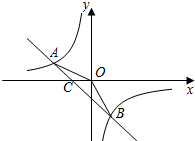 如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.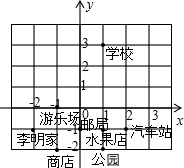 如图中标明了李明同学家附近的一些地方.
如图中标明了李明同学家附近的一些地方.