题目内容
17.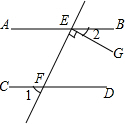 如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
分析 先根据对顶角相等求出∠EFD的度数,再由平行线的性质求出∠BEF的度数,根据EG⊥EF即可得出结论.
解答 解:∵∠1=50°,
∴∠EFD=∠1=50°.
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴∠BEF=180°-50°=130°.
∵EG⊥EF,
∴∠GEF=90°,
∴∠2=∠BEF-∠GEF
=130°-90°
=40°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
8.在实数:3.14159,$\root{3}{64}$,1.010010001…,4.21,π,$\frac{22}{7}$,3$\sqrt{2}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC:∠EOD=1:2,则∠BOD等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
7.(-2)n+2(-2)n-1的值是( )
| A. | 1 | B. | -1 | C. | 0 | D. | (-1)n+1 |
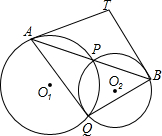 如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.
如图,⊙O1与⊙O2相交于P、Q两点,过P点作两圆的割线分别交于⊙O1与⊙O2于A、B,过A、B分别作两圆的切线相交于T,求证:T、A、Q、B四点共圆.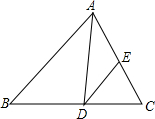 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.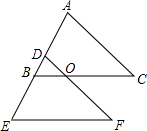 如图所示,△ABC平移后得到△DEF.
如图所示,△ABC平移后得到△DEF.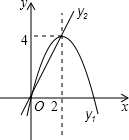 如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)
如图,已知抛物线y1=-x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.则①当x>4时,M<0;②当x<2时,M随着x增大而增大;③使得M大于4的x值不存在;④若M=2,则x=1,其中正确的有②③(填写序号)