题目内容
2.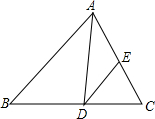 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,求∠ADE的度数.
分析 先根据三角形内角和定理求出∠BAC的度数,再由角平分线的性质求出∠BAD的度数,根据平行线的性质即可得出结论.
解答 解:∵在△ABC中,∠B=46°,∠C=54°,
∴∠BAC=180°-46°-54°=80°.
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=40°.
∵DE∥AB,
∴∠ADE=∠BAD=40°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
13.下面的等式总能成立的是( )
| A. | $\sqrt{{a}^{2}}$=a | B. | $\sqrt{{a}^{2}}$=a2 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{ab}$=$\sqrt{a}$$•\sqrt{b}$ |
7.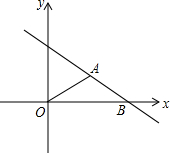 如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时PB的长为( )
如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时PB的长为( )
 如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时PB的长为( )
如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时PB的长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 6 |
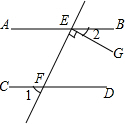 如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.
如图,直线AB∥CD,直线EF与AB、CD分别交于点E、F,EG⊥EF,垂足为E,若∠1=50°,求∠2的度数.